Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB = a
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB = a, \[{\rm{AD}} = a\sqrt 3 \], SA ⊥ (ABCD). Khoảng cách từ O đến mặt phẳng (SCD) bằng \(\frac{{a\sqrt 3 }}{4}\). Thể tích khối đa diện S.BCD là:
A. \(\frac{{{a^3}\sqrt 3 }}{6}\)
B. \(\frac{{{a^3}\sqrt 3 }}{3}\)
C. \(\frac{{{a^3}\sqrt {15} }}{{10}}\)
D. \({a^3}\sqrt 3 \).
Trả lời:
Đáp án đúng là: A
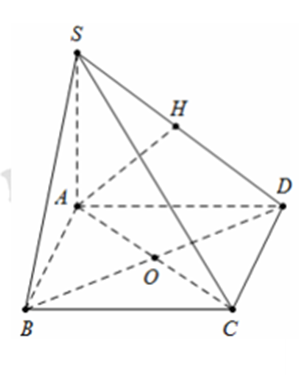
Kẻ AH ⊥ SD tại H
Ta có: \(\left\{ \begin{array}{l}SA \bot C{\rm{D}}\\A{\rm{D}} \bot C{\rm{D}}\end{array} \right. \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot AH\)
Suy ra AH ⊥ (SCD)
Do đó \[{\rm{d}}\left( {A;\left( {SC{\rm{D}}} \right)} \right) = AH\]
Mà \[{\rm{d}}\left( {A;\left( {SC{\rm{D}}} \right)} \right) = 2{\rm{d}}\left( {O;\left( {SC{\rm{D}}} \right)} \right) = \frac{{a\sqrt 3 }}{2} \Rightarrow AH = \frac{{a\sqrt 3 }}{2}\]
Vì tam giác SAD vuông tại A nên theo hệ thức lượng ta có
\(\begin{array}{l}\frac{1}{{S{A^2}}} + \frac{1}{{A{{\rm{D}}^2}}} = \frac{1}{{A{H^2}}}\\ \Leftrightarrow \frac{1}{{S{A^2}}} + \frac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} = \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}}\\ \Leftrightarrow SA = a\end{array}\)
Thể tích khối đa diện S.BCD là:
\({V_{S.BC{\rm{D}}}} = \frac{1}{3}SA.{S_{BC{\rm{D}}}} = \frac{1}{3}.a.\frac{1}{2}CB.B{\rm{D = }}\frac{1}{3}.a.\frac{1}{2}.a\sqrt 3 .a = \frac{{{a^3}\sqrt 3 }}{6}\)
Vậy ta chọn đáp án A.


