Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AD = 2AB = 2CD = 2a
Câu hỏi:
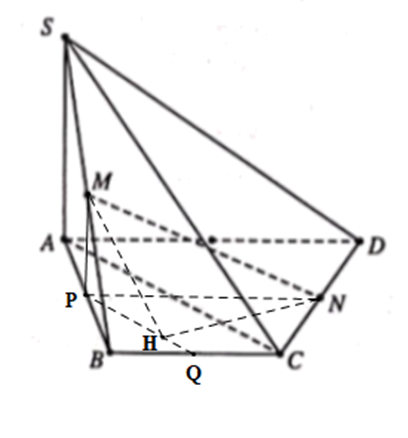
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AD = 2AB = 2CD = 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Gọi M, N lần lượt là trung điểm của SB và CD (tham khảo hình vẽ bên). Tính sin góc giữa MN và (SAC), biết thể tích khối chóp S.ABCD bằng \(\frac{{{a^3}\sqrt 3 }}{4}\).

A. \(\frac{{\sqrt 5 }}{{10}}\)
B. \(\frac{{3\sqrt {10} }}{{20}}\)
C. \(\frac{{\sqrt {10} }}{{20}}\)
D. \(\frac{{3\sqrt 5 }}{{10}}\).
Trả lời:
Đáp án đúng là: B
Diện tích hình thang cân ABCD là \({{\rm{S}}_{{\rm{ABCD}}}} = \frac{{3{{\rm{a}}^2}\sqrt 3 }}{4}\)
Mà \({V_{S.ABC{\rm{D}}}} = \frac{{{a^3}\sqrt 3 }}{4} \Rightarrow SA = a\)
Gọi P, Q lần lượt là trung điểm của AB, BC
Suy ra PQ là đường trung bình của tam giác ABC
Do đó PQ // AC \( \Rightarrow ({\rm{SAC}})\,{\rm{//}}\,({\rm{MPQ}}){\rm{ }}\)
Do đó: \(\widehat {\left( {{\rm{MN;}}\left( {SAC} \right)} \right)} = \widehat {\left( {MN;({\rm{MPQ}})} \right)} = (\widehat {{\rm{MN}};{\rm{NH}}}) = \widehat {{\rm{MNH}}}\) với H là hình chiếu của N trên PQ
Xét tam giác SAB có P, M lần lượt là trung điểm của AB, BS
Suy ra PM là đường trung bình
Do đó PM // SA \( \Rightarrow {\rm{MP}} \bot ({\rm{ABCD}})\)
Suy ra tam giác MPN vuông tại P
Khi đó \({\rm{MN}} = \sqrt {{\rm{M}}{{\rm{P}}^2} + {\rm{N}}{{\rm{P}}^2}} = \sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {{\left( {\frac{{3{\rm{a}}}}{2}} \right)}^2}} = \frac{{a\sqrt {10} }}{2}\) (định lý Pytago)
Ta có \({\rm{NH}} \bot {\rm{PQ}}\)
\( \Rightarrow {\rm{NH}} = \frac{3}{2}\;{\rm{d}}(\;{\rm{N}};({\rm{PQ}})) = \frac{3}{2}\;{\rm{d}}(\;{\rm{B}};({\rm{PQ}})) = \frac{3}{4}\)
Tam giác NMH vuông tại H, có \(\sin \widehat {MNH} = \frac{{NH}}{{MN}} = \frac{3}{4}:\frac{{\sqrt {10} }}{2} = \frac{{3\sqrt {10} }}{{20}}\)
Vậy ta chọn đáp án B.

