Có bao nhiêu giá trị nguyên dương của m để hàm số y = ln(x^3 - 3m2x + 72m)
Câu hỏi:
Có bao nhiêu giá trị nguyên dương của m để hàm số y = ln(x3 – 3m2x + 72m) xác định trên (0; +∞).
A. 10
B. 12
C. 6
D. 5
Trả lời:
Đáp án đúng là D
Hàm số y = ln(x3 – 3m2x + 72m) xác định trên (0; +∞)
\( \Leftrightarrow {x^3} - 3{m^2}x + 72m > 0,\forall x > 0\)
Xét hàm số \(f(x) = {x^3} - 3{m^2}x + 72m\)
Ta có
\(\begin{array}{l}f'(x) = 3{x^2} - 3{m^2}\\f'(x) = 0 \Leftrightarrow 3{x^2} - 3{m^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = m}\\{x = - m}\end{array}} \right.\end{array}\)
Với m nguyên dương ta có bảng biến thiên:
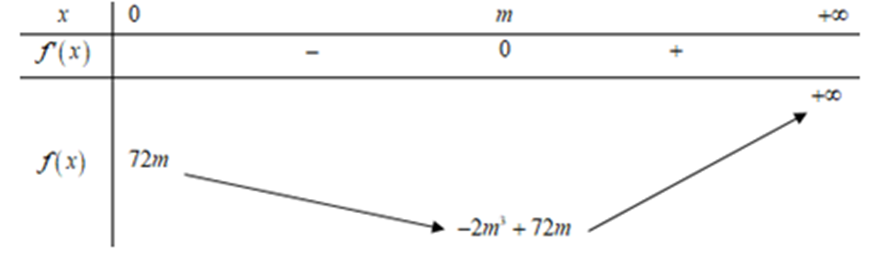
Do đó: \(f(x) > 0,\forall x > 0 \Leftrightarrow - 2{m^3} + 72m > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m < - 6}\\{0 < m < 6}\end{array}} \right.\)
Vì \(m \in {\mathbb{Z}^ + } \Rightarrow m \in \{ 1;2;3;4;5\} \)
Suy ra có 5 giá trị nguyên dương của m thỏa mãn yêu cầu bài toán
Vậy ta chọn đáp án D.
1122. log3(x cawnxx 3)


