Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Diện tích S của mặt cầu ngoại
Câu hỏi:
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Diện tích S của mặt cầu ngoại tiếp hình lập phương đó là:
A. S = πa2
B. \(S = \frac{{3\pi {a^2}}}{4}\)
C. S = 3πa2
D. S = 12πa2.
Trả lời:
Đáp án đúng là C
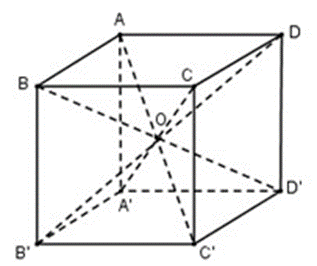
Vì ABCD là hình vuông nên AC = BD
Vì tam giác ABD vuông tại A nên \(B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}} \)
Suy ra \(AC = \sqrt {A{B^2} + A{{\rm{D}}^2}} \)
Vì tam giác AA’C’ vuông tại A’ nên \(AC' = \sqrt {AA{'^2} + A'C{'^2}} \)
Mà A’C’ = AC nên \(AC' = \sqrt {AA{'^2} + A{C^2}} \)
Hình lập phương ABCD.A’B’C’D’ có bán kính mặt cầu ngoại tiếp
\(R = \frac{1}{2}AC' = \frac{1}{2}\sqrt {A{C^2} + A'{A^2}} = \frac{1}{2}\sqrt {A{B^2} + A{D^2} + AA{'^2}} = \frac{1}{2}a\sqrt 3 \)
Diện tích mặt cầu đó là: \(S = 4\pi {R^2} = 4\pi .{\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = 3\pi {a^2}\)
Vậy ta chọn đáp án C.


