Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc BAD
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, \(\widehat {BAD} = 60^\circ ,\) \(SA = SB = SD = \frac{{a\sqrt 3 }}{2}.\) Gọi α là góc giữa hai mặt phẳng (SBD) và (ABCD). Mệnh đề nào sau đấy đúng?
A. \(\tan \alpha = \sqrt 5 .\)
B. \(\tan \alpha = \frac{{\sqrt 5 }}{5}.\)
C. \(\tan \alpha = \frac{{\sqrt 3 }}{2}.\)
D. \(\alpha = 45^\circ .\)
Trả lời:
Đáp án đúng là: A
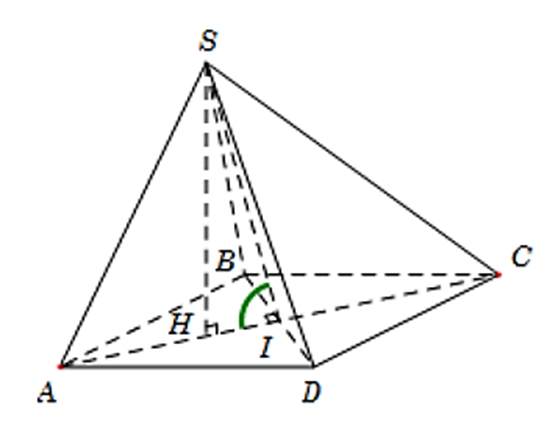
Từ giả thiết suy ra tam giác ABD đều cạnh a.
Gọi H là hình chiếu của S trên mặt phẳng (ABCD).
Do SA = SB = SD nên suy ra H là tâm của tam giác đều ABD.
⇒ \(\left\{ {\begin{array}{*{20}{c}}{AH = \frac{2}{3}.AI = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}}\\{HI = \frac{1}{3}.AI = \frac{1}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}}\\{SH = \sqrt {S{A^2} - A{H^2}} = \frac{{a\sqrt {15} }}{3}}\end{array}} \right.\)
Vì ABCD là hình thoi nên HI ⊥ BD. Tam giác SBD cân tại S nên SI ⊥ BD
⇒ \(\left( {\widehat {\left( {SBD} \right);\,\,\left( {ABCD} \right)}} \right) = \left( {\widehat {SI;\,\,AI}} \right) = \widehat {SIH}.\)
Trong tam giác vuông SHI, có \(\tan \widehat {SIH} = \frac{{SH}}{{HI}} = \sqrt 5 .\)

