Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = 2a. Gọi M là trung điểm của SD. Tính khoảng cách d giữa đường thẳng SB và mặt phẳng (ACM).
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = 2a. Gọi M là trung điểm của SD. Tính khoảng cách d giữa đường thẳng SB và mặt phẳng (ACM).
Trả lời:
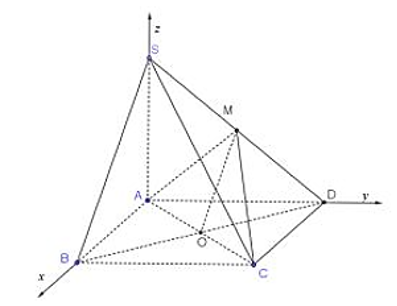
Chọn hệ trục tọa độ như hình vẽ, trong đó:
A(0; 0; 0); B(a; 0; 0); C(a; a; 0); D(0; a; 0); S(0; 0; 2a)
Vì M là trung điểm của SD nên M(0; a2; a)
Gọi O là giao điểm của AC, BD
Khi đó MO // SB nên SB // (ACM)
Do đó d(SB, (ACM)) = d(B, (ACM))
Ta có:
Suy ra là một vectơ chỉ phương của mặt phẳng (ACM).
Khi đó phương trình mặt phẳng (ACM): 2x – 2y + z = 0.
Do đó d(SB, (ACM)) = d(B, (ACM)) = .
Vậy khoảng cách d giữa đường thẳng SB và mặt phẳng (ACM) là .

