Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, góc BAD = 60 độ, SA = a và SA
Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, \[\widehat {BAD} = 60^\circ ,\] SA = a và SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng (SCD) bằng:
A. \(\frac{{\sqrt {21} a}}{7}\)
B. \(\frac{{\sqrt {15} a}}{7}\)
C. \(\frac{{\sqrt {21} a}}{3}\)
D. \(\frac{{\sqrt {15} a}}{3}\)
Trả lời:
Đáp án đúng là: A
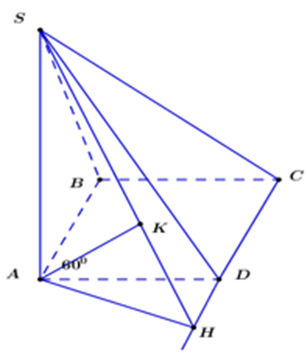
Ta có: AB // (SCD)
⇒ d(B; (SCD)) = d(A; (SCD)) = d
Kẻ AH ⊥ CD; AK ⊥ SH
\(\left\{ {\begin{array}{*{20}{c}}{CD \bot SA}\\{CD \bot AH}\end{array} \Rightarrow CD \bot \left( {SAH} \right)} \right.\)
⇒ CD ⊥ AK ⇒ AK ⊥ (SCD)
⇒ d(B; (SCD)) = d = AK.
Xét ∆AHD vuông tại H, \[\widehat {ADH} = 60^\circ \]
ta có: \(AH = AD \cdot {\rm{sin}}60^\circ = \frac{{a\sqrt 3 }}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông SHA vuông tại A có đường cao AK ta có: \(AK = \frac{{SA \cdot AH}}{{\sqrt {S{A^2} + A{H^2}} }}\)\( = \frac{{a \cdot \frac{{a\sqrt 3 }}{2}}}{{\sqrt {{a^2} + \frac{{3{a^2}}}{4}} }} = \frac{{a\sqrt {21} }}{7} = d.\)

