Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a. Tam giác
Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Biết thể tích khối chóp S.ABCD bằng \[\frac{{4{a^3}}}{3}\]. Gọi α là góc giữa SC và mặt đáy. Tính tan α.
Trả lời:
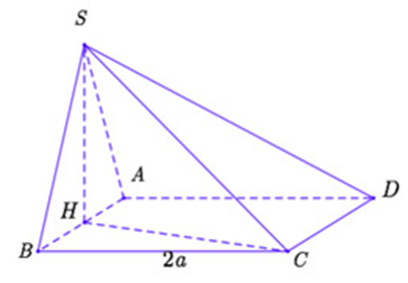
Gọi H là trung điểm của AB
Þ SH ⊥ AB (do ΔSAB cân tại S)
Ta có: (SAB) ⊥ (ABCD)
(SAB) ∩ (ABCD) = AB
SH ⊥ AB; SH ⊂ (SAB)
Þ SH ⊥ (ABCD)
Hay H là hình chiếu của S lên mặt phẳng (ABCD)
Þ CH là hình chiếu của SC lên mặt phẳng (ABCD)
Do đó góc giữa SC và mặt đáy là \[\widehat {SCH} = \alpha \].
Ta có:
\[{V_{S.ABCD}} = \frac{1}{3}SH.{S_{ABCD}}\]
\[ \Leftrightarrow \frac{{4{a^3}}}{3} = \frac{1}{3}SH.4{a^2} \Leftrightarrow SH = a\]
Xét tam giác BHC vuông tại B, theo định lý Py-ta-go, ta có:
\[HC = \sqrt {B{H^2} + B{C^2}} = \sqrt {{a^2} + 4{a^2}} = a\sqrt 5 \]
Xét tam giác SHC vuông tại H có:
\[\tan \widehat {SCH} = \frac{{SH}}{{HC}} = \frac{a}{{a\sqrt 5 }} = \frac{1}{{\sqrt 5 }}\]
Vậy \[\tan \widehat {SCH} = \frac{1}{{\sqrt 5 }}\].


