Cho hình chóp S.ABCD. Gọi M, N, P, Q lần lượt là trung điểm của SA, SB, SC, SD
Câu hỏi:
Cho hình chóp S.ABCD. Gọi M, N, P, Q lần lượt là trung điểm của SA, SB, SC, SD. Tính tỉ số thể tích của khối chóp S.MNPQ và khối chóp S.ABCD.
Trả lời:
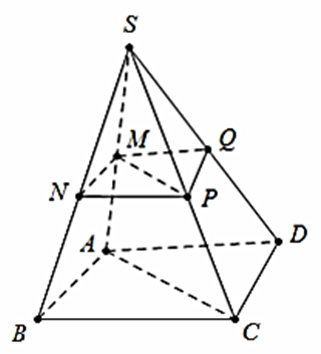
Ta có tỉ số: \(\frac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SA}} \cdot \frac{{SN}}{{SB}} \cdot \frac{{SP}}{{SC}} = \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{8}\)
\( \Rightarrow {V_{S.MNP}} = \frac{1}{8}{V_{S.ABC}}\)
Tương tự ta cũng có tỉ số:
\(\frac{{{V_{S.MPQ}}}}{{{V_{S.ACD}}}} = \frac{{SM}}{{SA}} \cdot \frac{{SP}}{{SC}} \cdot \frac{{SQ}}{{SD}} = \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{8}\)
\( \Rightarrow {V_{S.MPQ}} = \frac{1}{8}{V_{S.ACD}}\)
Do đó: \[{V_{S.MNPQ}} = {V_{S.MNP}} + {V_{S.MPQ}} = \frac{1}{8}{V_{S.ABC}} + \frac{1}{8}{V_{S.ACD}}\]
\[ = \frac{1}{8}\left( {{V_{S.ABC}} + {V_{S.ACD}}} \right) = \frac{1}{8}{V_{S.ABCD}}\]
\( \Rightarrow \frac{{{V_{S.MNPQ}}}}{{{V_{S.ABCD}}}} = \frac{1}{8}\).
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho a, b, c là các số thực dương thỏa mãn abc = 1. Tìm giá trị lớn nhất của biểu thức \(P = \frac{1}{{a + 2b + 3}} + \frac{1}{{b + 2c + 3}} + \frac{1}{{c + 2a + 3}}\).
Xem lời giải »
Câu 2:
Cho các số thực dương thỏa mãn a + b + c = 1. Tìm giá trị lớn nhất của biểu thức: \(P = \frac{a}{{\sqrt {a + bc} }} + \frac{b}{{\sqrt {b + ca} }} + \frac{c}{{\sqrt {c + ab} }}\).
Xem lời giải »
Câu 3:
Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy bằng a và cạnh bên bằng 2a. Tính thể tích của khối lăng trụ đã cho.
Xem lời giải »
Câu 4:
Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy và cạnh bên cùng bằng a. Tính thể tích của khối lăng trụ đó.
Xem lời giải »
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M và N theo thứ tự là trung điểm của SA và SB. Tính tỉ số thể tích \(\frac{{{V_{S.CDMN}}}}{{{V_{S.CDAB}}}}\).
Xem lời giải »
Câu 6:
Cho tứ diện ABCD có thể tích bằng V, hai điểm M và P lần lượt là trung điểm AB, CD điểm N thuộc AD sao cho AD = 3AN. Tính thể tích tứ diện BMNP.
Xem lời giải »
Câu 7:
Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB, CD và P là một điểm thuộc cạnh BC (P không trùng trung điểm cạnh BC). Tìm thiết diện của tứ diện cắt bởi mặt phẳng (MNP).
Xem lời giải »
Câu 8:
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc [−10; 10] để đồ thị hàm số \(y = \frac{{\sqrt {m{x^2} - 4} }}{{x - 1}}\) có ba đường tiệm cận?
Xem lời giải »


