Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng 2a
Câu hỏi:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng 2a. Diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp ABCD là:
A. \(\frac{{\pi {a^2}\sqrt {17} }}{8}\);
B. \(\frac{{\pi {a^2}\sqrt {15} }}{4}\);
C. \(\frac{{\pi {a^2}\sqrt {17} }}{6}\);
D. \(\frac{{\pi {a^2}\sqrt {17} }}{4}\).
Trả lời:
Đáp án đúng là: D
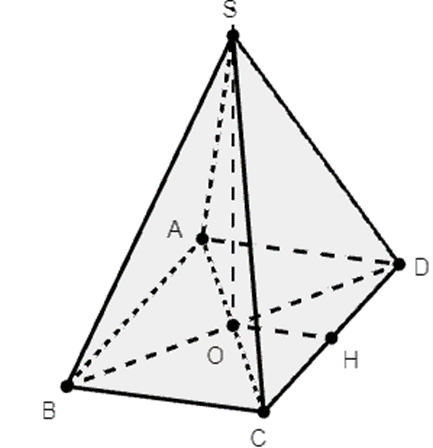
Ta có \(R = OH = \frac{a}{2}\)
\(SH = \sqrt {S{O^2} + O{H^2}} = \sqrt {{{\left( {2a} \right)}^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt {17} }}{2}\)
Vậy \({S_{xq}} = \pi .\frac{a}{2}.\frac{{a\sqrt {17} }}{2} = \frac{{\pi {a^2}\sqrt {17} }}{4}\)

