Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, biết
Câu hỏi:
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, biết BA = BC = 2a và (A’BC) hợp với đáy một góc 30°. Tính thể tích khối lăng trụ ABC.A’B’C’ là:
A. 6a3;
B. \(\frac{{4{a^3}\sqrt 3 }}{9}\);
C. \(4{a^3}\sqrt 3 \);
D. \(\frac{{4{a^3}\sqrt 3 }}{3}\).
Trả lời:
Đáp án đúng là: D
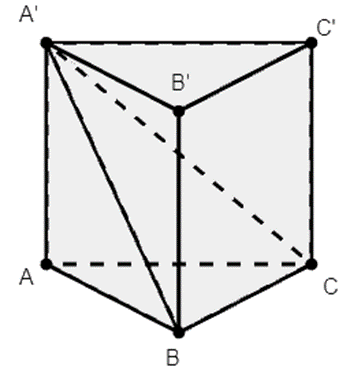
Ta có: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot AA'\end{array} \right. \Rightarrow BC \bot \left( {A'BA} \right) \Rightarrow \widehat {A'BA} = 30^\circ \)
Khi đó \(AA' = AB.\tan 30^\circ = \frac{{2a}}{{\sqrt 3 }}\)
\( \Rightarrow {V_{ABC.A'B'C'}} = {S_{ABC}}.AA' = \frac{{4{a^2}}}{2}.\frac{{2a}}{{\sqrt 3 }} = \frac{{4{a^3}\sqrt 3 }}{3}\)

