Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, tâm O và
Câu hỏi:
Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, tâm O và \(\widehat {ABC} = 120^\circ \). Các cạnh AA', A'B, A'D cùng tạo với đáy một góc 60°. Tính theo a thể tích V của khối lăng trụ đã cho.
A. \({a^3}\sqrt 3 \);
B. \(\frac{{{a^3}\sqrt 3 }}{6}\);
C. \(\frac{{{a^3}\sqrt 3 }}{2}\);
D. \(\frac{{3{a^2}}}{2}\).
Trả lời:
Đáp án đúng là: C
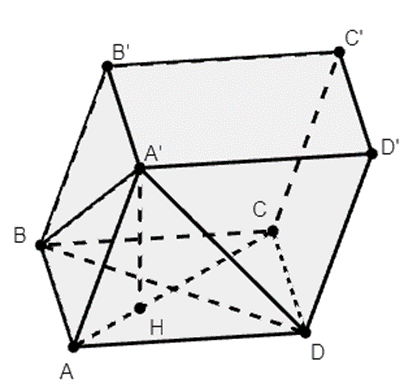
Ta có: \(\widehat {ABC} = 120^\circ \Rightarrow \widehat {BAD} = 60^\circ \) suy ra tam giác ABD là tam giác đều cạnh a.
Khi đó A’.ABD là chóp đều cạnh đáy bằng a.
Như vậy hình chiếu vuông góc của A’ lên mặt đáy trùng với trọng tam tam giác ABD.
Ta có: \(A'H = HA.\tan 60^\circ = \frac{{a\sqrt 3 }}{3}.\sqrt 3 = a\)
\( \Rightarrow {V_{A'.ABD}} = \frac{1}{3}A'H.{S_{ABC}} = \frac{{{a^3}\sqrt 3 }}{{12}}\)
Do đó \({V_{ABCD.A'B'C'D'}} = 3.{V_{A'.ABCD}} = 6.{V_{A'.ABD}} = \frac{{{a^3}\sqrt 3 }}{2}\).

