Cho hình chữ nhật ABCD, tâm O, AB = 4, BC = 3. I là trung điểm BC. Tính
Câu hỏi:
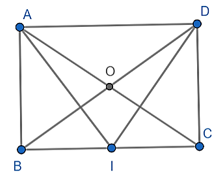
Cho hình chữ nhật ABCD, tâm O, AB = 4, BC = 3. I là trung điểm BC. Tính \(\left| {\overrightarrow {IA} - \overrightarrow {DI} } \right|;\left| {\overrightarrow {IA} + \overrightarrow {IB} } \right|\).
Trả lời:
\(\left| {\overrightarrow {IA} - \overrightarrow {DI} } \right| = \left| {\overrightarrow {IA} + \overrightarrow {ID} } \right| = \left| {\overrightarrow {IA} + \overrightarrow {IC} + \overrightarrow {CD} } \right| = \left| {\overrightarrow {IB} + \overrightarrow {BA} + \overrightarrow {BI} + \overrightarrow {BA} } \right| = 2\overrightarrow {BA} \)
(Vì \(\overrightarrow {IC} = \overrightarrow {BI} ;\overrightarrow {CD} = \overrightarrow {BA} \))
Suy ra: \(\left| {\overrightarrow {IA} - \overrightarrow {DI} } \right| = 2BA = 2.4 = 8\)
Lại có: \[\left| {\overrightarrow {IA} + \overrightarrow {IB} } \right| = \left| {\overrightarrow {IC} + \overrightarrow {CA} + \overrightarrow {IB} } \right| = \left| {\overrightarrow {BI} + \overrightarrow {CA} + \overrightarrow {IB} } \right| = \left| {\overrightarrow {CA} } \right| = CA\]
Mà: \(CA = \sqrt {A{B^2} + B{C^2}} = 5\)
Suy ra: \(\left| {\overrightarrow {IA} + \overrightarrow {IB} } \right| = CA = 5.\)

