Cho tam giác đều cạnh a. Tính |vecto AB - veco AC|; |vecto AB + vecto AC|
Câu hỏi:
Cho tam giác đều cạnh a. Tính \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|;\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\).
Trả lời:
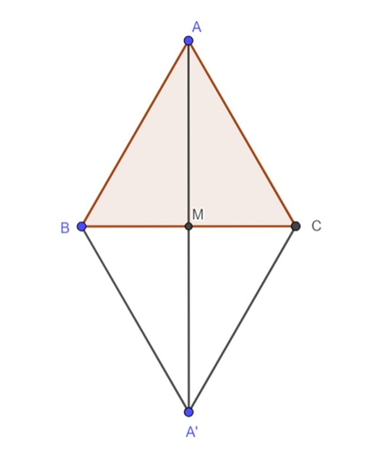
Dựng ABA'C là hình bình hành, M là trung điểm của BC, nên M cũng là trung điểm của AA')
Có AM là đường cao trong tam giác đều ABC
\(AM = \sqrt {A{B^2} - B{M^2}} = \sqrt {A{B^2} - {{\left( {\frac{1}{2}BC} \right)}^2}} = \sqrt {{a^2} - \frac{{{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}\)
\(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = a\)
\(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AA'} } \right| = 2\left| {\overrightarrow {AM} } \right| = 2AM = 2.\frac{{a\sqrt 3 }}{2} = a\sqrt 3 \).

