Cho hình lăng trụ ABC. A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông
Câu hỏi:
Cho hình lăng trụ ABC. A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA' và BC bằng \[a\sqrt {34} \]. Tính theo a thể tích V của khối lăng trụ ABC. A'B'C'.
A. \(\frac{{{a^3}\sqrt 3 }}{6}.\)
B. \(\frac{{{a^3}\sqrt 3 }}{{12}}.\)
C. \(\frac{{{a^3}\sqrt 3 }}{3}.\)
D. \(\frac{{{a^3}\sqrt 3 }}{{24}}.\)
Trả lời:
Đáp án đúng là: B
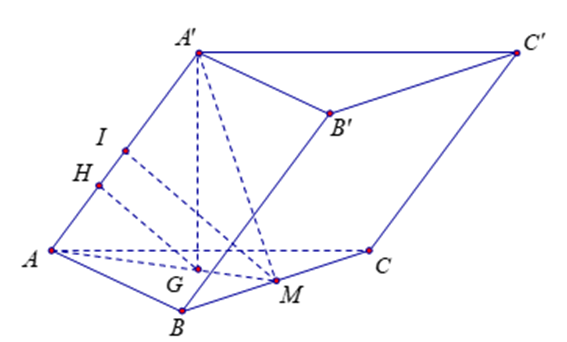
Gọi G là trọng tâm tam giác ABC và M là trung điểm của BC.
Ta có A'G ⊥ (ABC) nên A'G ⊥ BC; BC ⊥ AM ⇒ BC ⊥ (MAA')
Kẻ MI ⊥ AA' ; BC ⊥ IM nên \[d\left( {{\rm{AA';BC}}} \right) = IM = \frac{{a\sqrt 3 }}{4}.\]
Kẻ GH ⊥ AA', ta có:
\(\frac{{AG}}{{AM}} = \frac{{GH}}{{IM}} = \frac{2}{3} \Leftrightarrow GH = \frac{2}{3} \cdot \frac{{a\sqrt 3 }}{4} = \frac{{a\sqrt 3 }}{6}\)
\(\frac{1}{{H{G^2}}} = \frac{1}{{A'{G^2}}} + \frac{1}{{A{G^2}}} \Leftrightarrow A'G = \frac{{AG \cdot HG}}{{\sqrt {A{G^2} - H{G^2}} }} = \frac{{\frac{{a\sqrt 3 }}{3} \cdot \frac{{a\sqrt 3 }}{6}}}{{\sqrt {\frac{{{a^2}}}{3} - \frac{{{a^2}}}{{12}}} }} = \frac{a}{3}\)
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hai tập hợp X = {1; 2; 3; 4}; Y = {1;2}. Tập hợp CXY là tập hợp nào sau đây?
Xem lời giải »
Câu 3:
Giá trị của biểu thức A=tan1°tan2°tan3°...tan88°tan89° là:
Xem lời giải »
Câu 5:
Có bao nhiêu số nguyên x thỏa mãn (x ‒ 7)(x + 5) < 0 ?
Xem lời giải »
Câu 6:
Phương trình \(\sqrt 3 {\rm{sin}}2x - {\rm{cos}}2x + 1 = 0\) có nghiệm là:
Xem lời giải »
Câu 7:
Cho hai hàm số f(x) và g(x) cùng đồng biến trên khoảng (a; b). Có thể kết luận gì về chiều biến thiên của hàm số y = f(x) + g(x) trên khoảng (a; b)?
Xem lời giải »
Câu 8:
Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipid trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipid. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipid. Biết rằng gia đình này chỉ mua nhiều nhất là 1,6kg thịt bò và 1,1kg thịt lợn; giá tiền 1kg thịt bò là 250 nghìn đồng; 1kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.
a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó.
b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy biểu diễn F theo x và y.
c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.
Xem lời giải »


