Cho hình lăng trụ đều ABC.A'B'C' , biết góc giữa hai mặt phẳng (A'BC) và (A'B'C')
Câu hỏi:
Cho hình lăng trụ đều ABC.A'B'C' , biết góc giữa hai mặt phẳng (A'BC) và (A'B'C') bằng 45°, diện tích tam giác A'BC bằng \({a^2}\sqrt 6 \). Tính diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ.
Trả lời:
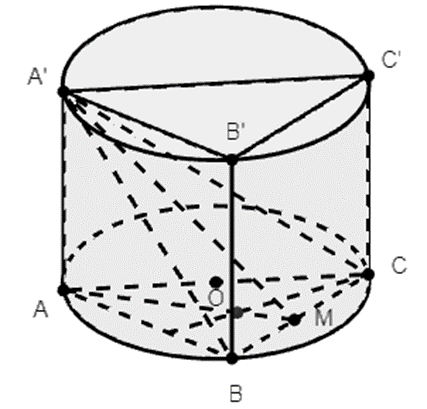
Gọi M là trung điểm BC.
Khi đó ta có: BC ⊥ AM, BC ⊥ A’M.
Suy rs: ((A’BC), (ABC)) = \(\widehat {A'MA} = 45^\circ \) ⇒ A’A = AM.
Gọi O là trọng tâm tam giác ABC.
Đặt BC = x, x > 0.
Ta có \(AM = A'A = \frac{{x\sqrt 3 }}{2}\) \( \Rightarrow A'M = \frac{{x\sqrt 6 }}{2}\).
Nên \({S_{\Delta A'BC}} = \frac{1}{2}.A'M.BC = \frac{{{x^2}\sqrt 6 }}{4} = {a^2}\sqrt 6 \)
⇒ x = 2a.
Khi đó: \(AO = \frac{2}{3}AM = \frac{2}{3}.\frac{{2a\sqrt 3 }}{2} = \frac{{2a\sqrt 3 }}{3}\) và \(A'A = a\sqrt 3 \)
Suy ra diện tích xung quanh khối trụ là:
\({S_{xq}} = 2\pi \,.\,OA\,.\,A'A = 2\pi \frac{{2a\sqrt 3 }}{3}\,.\,a\sqrt 3 = 4\pi {a^2}\).

