Cho hình lăng trụ đứng ABC. A'B'C' có đáy ABC là tam giác đều cạnh a
Câu hỏi:
Cho hình lăng trụ đứng ABC. A'B'C' có đáy ABC là tam giác đều cạnh a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (A'BC) bằng \[\frac{a}{6}\]Thể tích khối lăng trụ bằng
Mệnh đề nào đúng?
A. \(\frac{{3{a^3}\sqrt 2 }}{4}.\)
B. \(\frac{{3{a^3}\sqrt 2 }}{8}.\)
C. \(\frac{{3{a^3}\sqrt 2 }}{{28}}.\)
D. \(\frac{{3{a^3}\sqrt 2 }}{{16}}.\)
Trả lời:
Đáp án đúng là: D
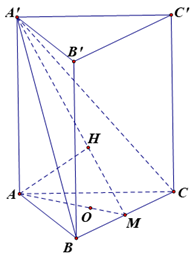
Gọi M là trung điểm của BC và H là hình chiếu của A trên A’M.
Ta có :
\(\left. {\begin{array}{*{20}{c}}{BC \bot AM}\\{BC \bot AA'}\end{array}} \right\}\) ⇒ BC ⊥ (AA’M) ⇒ BC ⊥ AH (1).
Mà AH ⊥ A’M (2).
Từ (1) và (2) ⇒ d(A, (A’BC)) = AH.
Ta có: \(\frac{{d\left( {O,\left( {A'BC} \right)} \right)}}{{d\left( {A,\left( {A'BC} \right)} \right)}} = \frac{{MO}}{{MA}} = \frac{1}{3}\) (do tính chất trọng tâm).
\( \Rightarrow d\left( {A,\left( {A'BC} \right)} \right) = 3d\left( {O,\left( {A'BC} \right)} \right) = \frac{a}{2}\)
\( \Rightarrow AH = \frac{a}{2}\)
Xét tam giác vuông A'AM :
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{A^{{\rm{'}}2}}}} + \frac{1}{{A{M^2}}}\)
\( \Leftrightarrow \frac{1}{{A{A^{{\rm{'}}2}}}} = \frac{4}{{{a^2}}} - \frac{4}{{3{a^2}}} \Leftrightarrow AA' = \frac{{a\sqrt 3 }}{{2\sqrt 2 }}\)
Suy ra thể tích lăng trụ ABC.A’B’C’ là:
\(V = AA' \cdot {S_{\Delta ABC}} = \frac{{a\sqrt 3 }}{{2\sqrt 2 }} \cdot \frac{{{a^2}\sqrt 3 }}{4} = \frac{{3\sqrt 2 {a^3}}}{{16}}.\)

