Cho hình lăng trụ tứ giác ABCD.A’B’C’D’ có đáy ABCD là hình vuông tâm là I và có diện tích bằng 9a^2.

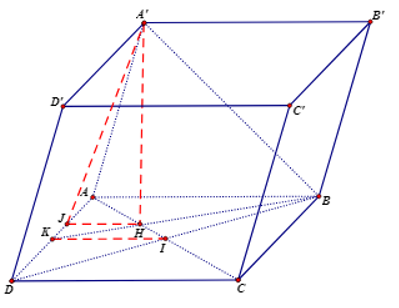
Cho hình lăng trụ tứ giác ABCD.A’B’C’D’ có đáy ABCD là hình vuông tâm là I và có diện tích bằng 9a2. Hình chiếu của đỉnh A’ trên mặt đáy (ABCD) là điểm H thỏa mãn $3\overrightarrow{AH}-2\overrightarrow{AI}=\overrightarrow{0}$ . Biết rằng $B=a\sqrt{6}$ . Tính góc giữa mặt phẳng (ADA’) và mặt phẳng (ABCD)

Đáp án đúng là: A

Xét tam giác ABD có $3\overrightarrow{AH}-2\overrightarrow{AI}=\overrightarrow{0}$  và AI là trung tuyến nên H là trọng tâm tam giác

Kéo dài BH cắt AD tại K

Suy ra K là trung điểm của AD và $BH=\frac{2}{3}BK$

Vì S_ABCD = 9a² nên AB = BC = CD = DA = 3a

Xét tam giác ABK vuông ở A có BK² = AB² + AK²

Suy ra $BK=\sqrt{A{B}^2+A{K}^2}=a\sqrt{5}$

Trong mp(ABCD) dựng HJ // AB (J ∈ AD)

Suy ra AD ⊥ HJ               (1)

Mà AD ⊥ HA’, do đó AD ⊥ (A’HJ)

Suy ra AD ⊥ A’J                       (2)

Ta có (A’AD) ∩ (ABCD) = AD                    (3)

Từ (1), (2) và (3) suy ra $\left(\left(A^{\text{'}}A\text{D}\right),\left(ABC\text{D}\right)\right)=\widehat{A\text{'}JH}$

Xét tam giác A’HB vuông tại H có A’B² = HB² + A’H²

Suy ra $A^{\text{'}}H=\sqrt{A^{\text{'}}{B}^2-H{B}^2}=\sqrt{{\left(\text{a}\sqrt{6}\right)}^2-{\left(a\sqrt{5}\right)}^2}=a$

Xét tam giác AKI có KI // JH

Suy ra $\frac{JH}{KI}=\frac{AH}{AI}=\frac{2}{3}$

Do đó $JH=\frac{2}{3}KI=a$

Xét tam giác A’HB vuông tại H có JH = A’H = a

Suy ra tam giác A’HJ vuông cân tại H

Do đó $\left(\left(A\text{'}A\text{D}\right),\left(ABC\text{D}\right)\right)=\widehat{A^{\text{'}}JH}=45°$

Vậy ta chọn đáp án A.