Cho hình nón đỉnh S có đáy là hình tròn tâm O. Một mặt phẳng đi qua đỉnh hình
Câu hỏi:
Cho hình nón đỉnh S có đáy là hình tròn tâm O. Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo một thiết diện là tam giác vuông SAB có diện tích bằng 4a2. Góc giữa trục SO và mặt phẳng (SAB) bằng 30°. Tính diện tích xung quanh của hình nón đã cho.
Trả lời:
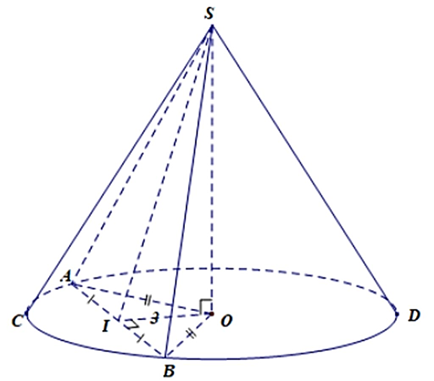
ΔSAB có SA = SB đều là đường sinh nên ΔSAB ⊥ cân đỉnh S.
Gọi I là trung điểm của AB
⇒ SI ⊥ AB, \(SI = \frac{{AB}}{2}\)
Áp dụng hệ thức lượng vào ΔSIO vuông tại O:
cos\[\widehat {ISO} = \frac{{SO}}{{SI}}\] ⇒ SI = \(\frac{{SO}}{{\cos 30^\circ }}\)
⇒ AB =\(\frac{{2SO}}{{\cos 30^\circ }}\)
SSAB = \(\frac{1}{2}.SI.AB = \frac{{S{O^2}}}{{{{\cos }^2}30^\circ }} = 4{a^2}\)
⇒ SO = \(a\sqrt 3 \)
⇒ AI = \(\frac{{AB}}{2} = 2a\)
IO = SO.tan30° = a
Áp dụng định lý Pytago vào tam giác OAI và SOA vuông ta có:
AO = \(\sqrt {A{I^2} + I{O^2}} = a\sqrt 5 \)
AS = \(\sqrt {S{O^2} + O{A^2}} = 2a\sqrt 2 \)
Sxq = π.OA.SA = π.\[a\sqrt 5 .2a\sqrt 2 = 2\pi {a^2}\sqrt {10} \].

