Cho hình trụ có hai đáy là hai hình tròn (O; R) và (O′; R). AB là một dây cung của
Câu hỏi:
Cho hình trụ có hai đáy là hai hình tròn (O; R) và (O′; R). AB là một dây cung của đường tròn (O; R) sao cho tam giác O′AB là tam giác đều và mặt phẳng (O′AB) tạo với mặt phẳng chứa đường tròn (O; R) một góc \(60^\circ .\) Tính theo R thể tích V của khối trụ đã cho.
Trả lời:
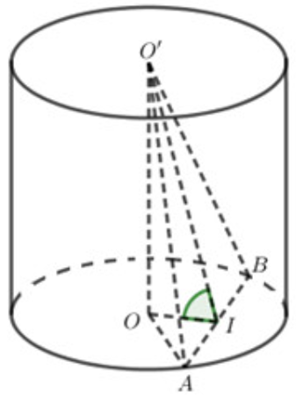
Gọi I là trung điểm của AB thì O′I ⊥ AB, OI ⊥ AB.
Suy ra góc giữa (O′AB) và (O; R) là góc giữa O′I và OI hay \(\widehat {O'IO} = 60^\circ .\)
Đặt AI = x ⇒ AB = 2x.
Tam giác vuông OIA có OA = R, AI = x
⇒ \(OI = \sqrt {O{A^2} - A{I^2}} = \sqrt {{R^2} - {x^2}} .\)
Tam giác O′AB đều cạnh AB = 2x ⇒ \(O'I = \frac{{2x\sqrt 3 }}{2} = x\sqrt 3 .\)
Tam giác O′OI vuông tại O nên \(\cos 60^\circ = \frac{{OI}}{{O'I}}\)
⇔ \(\frac{1}{2} = \frac{{\sqrt {{R^2} - {x^2}} }}{{x\sqrt 3 }}\) ⇔ \(x = \frac{{2R}}{{\sqrt 7 }}.\)
Suy ra \(OO' = O'I.\sin 60^\circ = \frac{{2R}}{{\sqrt 7 }}.\sqrt 3 .\frac{{\sqrt 3 }}{2} = \frac{{3R\sqrt 7 }}{7}.\)
Thể tích khối trụ \(V = \pi {R^2}h = \pi {R^2}.\frac{{3R\sqrt 7 }}{7} = \frac{{3\pi \sqrt 7 {R^3}}}{7}.\)

