Cho khối chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = a căn bậc hai 3
Câu hỏi:
Cho khối chóp S.ABCD có đáy là hình chữ nhật, \[AB = a,\;\] \(A{\rm{D}} = a\sqrt 3 ,\) SA vuông góc với đáy và mặt phẳng (SBC) tạo với đáy một góc 60°. Tính thể tích V của khối chóp S.ABCD.
A. V = a3
B. \(V = \frac{{{a^3}}}{3}\)
C. V = 3a3
D. \(V = \frac{{\sqrt 3 {a^3}}}{3}\).
Trả lời:
Đáp án đúng là: A
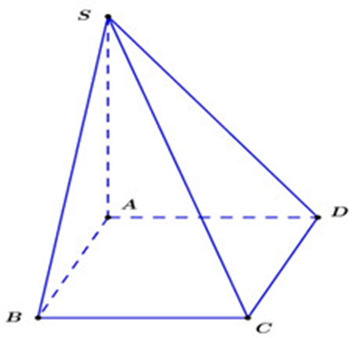
Ta có (ABCD) ∩ (SBC) = BC
Lại có \(\left\{ \begin{array}{l}AB \bot BC\\SA \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\)
Suy ra BC ⊥ SB
Do đó\(\left\{ \begin{array}{l}SB \bot BC\\BA \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right),\left( {ABC{\rm{D}}} \right)} \right)} = \widehat {\left( {SB,AB} \right)} = \widehat {SBA} = 60^\circ \)
Xét tam giác SAB ta có:
\(SA = AB.\tan 60^\circ = a\sqrt 3 \)
Tính thể tích V của khối chóp S.ABCD là
\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}SA.AB.A{\rm{D}} = \frac{1}{3}a\sqrt 3 .a.a\sqrt 3 = {a^3}\)
Vậy ta chọn đáp án A.

