Cho khối trụ có chiều cao h = 8, bán kính đường tròn đáy bằng 6, cắt khối trụ bởi
Câu hỏi:
Cho khối trụ có chiều cao h = 8, bán kính đường tròn đáy bằng 6, cắt khối trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng 4. Tính diện tích thiết diện tạo thành.
Trả lời:
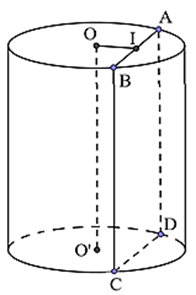
Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng 4 < R (R = 6).
Suy ra thiết diện là hình chữ nhật.
Giả sử thiết diện là hình chữ nhật ABCD (như hình vẽ), gọi I là trung điểm của AB.
Theo đề bài ta có:
OI = d(OO'; (ABCD)) = 4, BC = h = 8, R = 6
Tam giác OIA vuông tại I
\( \Rightarrow IA = \sqrt {O{A^2} - O{I^2}} = \sqrt {{6^2} - {4^2}} = 2\sqrt 5 \).
Diện tích của thiết diện là:
\({S_{ABCD}} = AB\,.\,BC = 4\sqrt 5 \,.\,8 = 32\sqrt 5 \).

