Cho một cây nến hình lăng trụ lục giác đều có chiều cao và độ dài cạnh đáy lần lượt
Câu hỏi:
Cho một cây nến hình lăng trụ lục giác đều có chiều cao và độ dài cạnh đáy lần lượt là 15 cm và 5 cm. Người ta xếp cây nến trên vào trong một hộp có dạng hình hộp chữ nhật sao cho cây nến nằm khít trong hộp (có đáy tiếp xúc như hình vẽ).
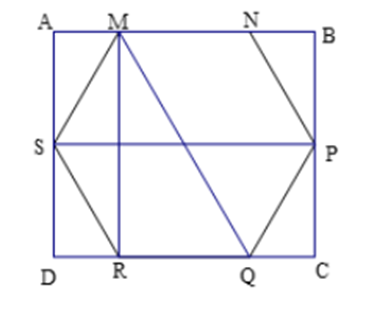
Thể tích của chiếc hộp đó bằng:
A. 1 500 cm3
B. \(600\sqrt 6 \) cm3
C. 1 800 cm3
D. \(750\sqrt 3 \) cm3.
Trả lời:
Đáp án đúng là: D
Ta có
AB = SP = 2MN = 10 cm
\[{\rm{AD}} = MR = 2\sqrt {{5^2} - {{\left( {\frac{5}{2}} \right)}^2}} = 5\sqrt 3 \]
Suy ra \[{{\rm{S}}_{ABC{\rm{D}}}} = AB.A{\rm{D}} = 10.5\sqrt 3 = 50\sqrt 3 \]
Thể tích của chiếc hộp đó bằng:
\(V = h.{S_{ABC{\rm{D}}}} = 15.50\sqrt 3 = 750\sqrt 3 \left( {c{m^3}} \right)\)
Vậy ta chọn đáp án D.

