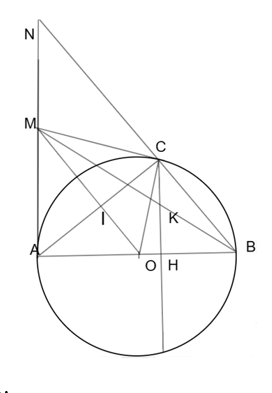
Cho nửa đường tròn (O) đường kính AB, kẻ tiếp tuyến Ax. Qua C nằm trên đường tròn kẻ tiếp tuyến với nửa đường tròn cắt Ax tại M, tia Bx cắt Ax tại N. a) Chứng minh OM vuông góc với AC.
Câu hỏi:
Cho nửa đường tròn (O) đường kính AB, kẻ tiếp tuyến Ax. Qua C nằm trên đường tròn kẻ tiếp tuyến với nửa đường tròn cắt Ax tại M, tia Bx cắt Ax tại N.
a) Chứng minh OM vuông góc với AC.
Trả lời:
a) Xét DMAO và DMCO có:
MA = MC
MO: chung
AO = AC
Do đó DMAO = DMCO (c.c.c).
Suy ra (hai góc tương ứng).
Nên OM là phân giác mà tam giác AOC cân tại O.
Do đó OM là đường cao của DAOC.
Vậy OM ^ AC.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Hình chữ nhật có nửa chu vi là 99 m. Nếu tăng chiều rộng thêm 5 m và giảm chiều dài đi 5 m thì diện tích không thay đổi. Tính chiều dài và chiều rộng.
Xem lời giải »
Câu 2:
Tìm số dư của phép chia 158 : 2,8 nếu chỉ lấy đến hai chữ số ở phần thập phân của thương.
Xem lời giải »
Câu 3:
Tìm số tự nhiên a, b biết ƯCLN(a, b) = 4 và a + b = 48.
Xem lời giải »
Câu 4:
Tính diện tích hình thoi có chu vi 52 cm, một đường chéo bằng 24 cm
Xem lời giải »
Câu 6:
c) Kẻ CH vuông góc AB, BM cắt CH ở K. Chứng minh K là trung điểm của CH.
Xem lời giải »
Câu 8:
Cho 10k - 1 chia hết cho 19 với k > 1. Chứng minh rằng:
a) 102k - 1 chia hết cho 19.
Xem lời giải »