Cho nửa đường tròn (O; R) đường kính AB, vẽ hai tiếp tuyến Ax, By với nửa đường tròn. Trên tia Ax lấy điểm E (E khác A, AE < R), trên nửa đường tròn lấy điểm M sao cho EM = EA, đường thẳng EM
Câu hỏi:
Cho nửa đường tròn (O; R) đường kính AB, vẽ hai tiếp tuyến Ax, By với nửa đường tròn. Trên tia Ax lấy điểm E (E khác A, AE < R), trên nửa đường tròn lấy điểm M sao cho EM = EA, đường thẳng EM cắt tia By tại F.
a) Chứng minh EF là tiếp tuyến của đường tròn (O).
b) Chứng minh tam giác EOF là tam giác vuông.
c) Chứng minh AM.OE + BM.OF = AB.EF.
d) Tìm vị trí điểm E trên tia Ax sao cho \({S_{\Delta AMB}} = \frac{3}{4}{S_{\Delta EOF}}\).
Trả lời:
Lời giải
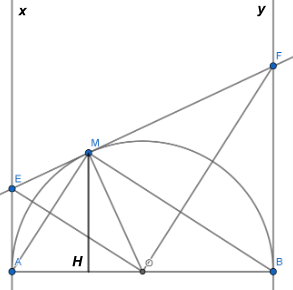
a) Xét ∆AOE và ∆MOE, có:
AO = MO = R;
AE = ME (giả thiết);
OE chung.
Do đó ∆AOE = ∆MOE (c.c.c).
Suy ra \(\widehat {EAO} = \widehat {EMO} = 90^\circ \).
Vậy EF là tiếp tuyến của đường tròn (O).
b) Ta có MF, BF là hai tiếp tuyến của (O).
Suy ra OF là tia phân giác của \(\widehat {MOB}\).
Do đó \(\widehat {MOF} = \widehat {BOF} = \frac{1}{2}\widehat {MOB}\).
Chứng minh tương tự, ta được \(\widehat {AOE} = \widehat {EOM} = \frac{1}{2}\widehat {AOM}\).
Ta có \(\widehat {AOM} + \widehat {MOB} = 180^\circ \) (kề bù).
\( \Rightarrow 2\widehat {EOM} + 2\widehat {MOF} = 180^\circ \).
\( \Rightarrow 2\left( {\widehat {EOM} + \widehat {MOF}} \right) = 180^\circ \).
\( \Rightarrow \widehat {EOF} = 180^\circ :2 = 90^\circ \).
Vậy tam giác EOF vuông tại O.
c) Ta có EA = EM (giả thiết) và OM = OA (= R).
Suy ra OE là đường trung trực của đoạn AM.
Do đó OE ⊥ AM.
Mà MA ⊥ MB (\(\widehat {AMB} = 90^\circ \) do \(\widehat {AMB}\) là góc nội tiếp chắn nửa đường tròn (O)).
Vì vậy OE // MB.
Suy ra \(\widehat {MOE} = \widehat {OMB}\) (so le trong).
Mà \(\widehat {ABM} = \widehat {OMB}\) (do tam giác OMB cân tại O).
Do đó \(\widehat {MOE} = \widehat {ABM}\).
Mà \(\widehat {EMO} = \widehat {AMB} = 90^\circ \).
Vì vậy (g.g).
Suy ra \(\frac{{EM}}{{AM}} = \frac{{OE}}{{AB}}\).
Do đó EM.AB = AM.OE (1)
Chứng minh tương tự, ta được FM.AB = BM.OF (2)
Từ (1), (2), suy ra AM.OE + BM.OF = AB.(EM + FM) = AB.EF.
Vậy ta có điều phải chứng minh.
d) Kẻ MH ⊥ AB tại H.
Ta có \(\widehat {MBA} = \widehat {OFB}\) (cùng phụ với \(\widehat {FOB}\)).
Mà \(\widehat {OFM} = \widehat {OFB}\) (do FO là tia phân giác của \(\widehat {MFB}\)).
Suy ra \(\widehat {MBA} = \widehat {OFE}\).
Mà \(\widehat {AMB} = \widehat {OEF} = 90^\circ \).
Do đó (g.g).
Suy ra \(\frac{{{S_{AMB}}}}{{{S_{EOF}}}} = {\left( {\frac{{MH}}{{OM}}} \right)^2} = \frac{3}{4}\).
Khi đó \(\frac{{MH}}{{OM}} = \frac{{\sqrt 3 }}{2}\).
Vì vậy \(\sin \widehat {MOH} = \frac{{\sqrt 3 }}{2}\).
Suy ra \(\widehat {MOH} = 60^\circ \).
Do đó \(\widehat {MOE} = \widehat {AOE} = 30^\circ \).
Ta có \(AE = OA.\tan \widehat {AOE} = OA.\tan 30^\circ = \frac{{\sqrt 3 }}{3}OA\).
Vậy E nằm trên tia Ax sao cho \(AE = \frac{{\sqrt 3 }}{3}OA\) thỏa mãn yêu cầu bài toán.

