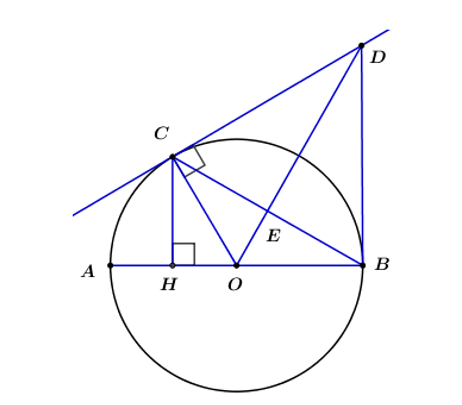
Cho (O) đường kính AB. Lấy C thuộc (O), gọi E là trung điểm BC. Tiếp tuyến tại C của (O) cắt OE ở D. Chứng minh: ΔACB vuông và OE ⊥ BC.

Khẳng định nào sau đây sai?

Câu nào trong các câu sau không phải là mệnh đề?

Cho hình thang ABCD vuông góc tại A và B, có AD = 2a, AB = BC = a. Trên tia Ax vuông góc với mặt phẳng (ABCD) lấy một điểm S. Gọi C’, D’ lần lượt là hình chiếu vuông góc của A trên SC và SD. Chứng minh rằng $\widehat{SBC}=\widehat{SCD}=90°$.

Cho đường tròn tâm O có đường kính AB và C là một điểm thuộc đường tròn tâm O (C khác A, B). Lấy điểm D thuộc dây cung BC (D khác B, C). Tia AD cắt cung nhỏ BC tại điểm E, tia AC cắt tia BE tại điểm F. Chứng minh tứ giác FCDE nội tiếp.

Cho x; y; z > 1 thỏa mãn  $\left\{\begin{array}{l}x=2y=3z\\ xy+yz+xz={12}^2\end{array}\right.\iff \left\{\begin{array}{l}x=12\\ y=6\\ z=4\end{array}\right.$. Tính x + y – z.

Cho (x + 2)ⁿ = a₀ + a₁x + a₂x² +...+ a_nxⁿ. Tìm a_n để a₅ : a₆ = 12 : 7.

Cho hàm số  $f\left(x\right)=\frac{a}{x^2}+\frac{b}{x}+2$ với a, b là các số hữu tỉ thỏa điều kiện  $\underset{\frac{1}{2}}{\overset{1}{\int }}f\left(x\right)dx=2-3\ln 2$. Tính T = a + b.