Cho (O; R) và (O; R') tiếp xúc ngoài tại A. Kẻ dây cung AM của (O) và dây cung AN của (O') sao cho AM vuông góc với AN. Chứng minh: a) OM song song O'N; b) Xác định vị trí của AM và AN để d

Cho (O; R) và (O; R') tiếp xúc ngoài tại A. Kẻ dây cung AM của (O) và dây cung AN của (O') sao cho AM vuông góc với AN. Chứng minh:

a) OM song song O'N;

b) Xác định vị trí của AM và AN để diện tích tứ giác OMNO' lớn nhất.

Lời giải         

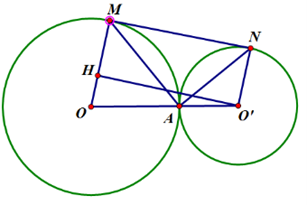
Xét ∆MAN vuông tại A có: \(\widehat {AMN} + \widehat {ANM} = 90^\circ \) (1)

Và \[\widehat {MAO} + \widehat {NAO'} = 90^\circ = 180^\circ - \widehat {MAO} = 180^\circ - 90^\circ = 90^\circ \] (2)

Lại có: ∆OMA cân tại O (OA = OM = R) ⟹ \[\widehat {OAM} = \widehat {OMA}\] (3)

∆O’NA cân tại O (O’A = O’N = R’) ⟹ \[\widehat {O'AN} = \widehat {O'NA}\](4)

Từ (1), (2), (3) và (4) suy ra:

\[\widehat {OMN} + \widehat {MNO'} = \left( {\widehat {OMA} + \widehat {AMN}} \right) + \left( {\widehat {ANM} + \widehat {O'NA}} \right)\]

\[ = \widehat {OMA} + \widehat {AMN} + \widehat {ANM} + \widehat {O'NA}\]

\[ = \widehat {OAM} + \widehat {AMN} + \widehat {ANM} + \widehat {O'AN}\]

\[ = \left( {\widehat {OAM} + \widehat {O'AN}} \right) + \left( {\widehat {AMN} + \widehat {ANM}} \right)\]

\[ = 90^\circ + 90^\circ \]

\[ = 180^\circ \]

Tứ giác OMNO’ có \[\widehat {OMN} + \widehat {MNO'} = 180^\circ \] nên MN // O’N.

b) Từ O’ kẻ O’H ⊥ OM. Khi đó:

\({S_{OMNO'}} = \frac{{\left( {O'N + OM} \right).O'H}}{2} = \frac{{\left( {R' + R} \right).O'H}}{2} \le \frac{{\left( {R' + R} \right).O'O}}{2} = \frac{{{{\left( {R' + R} \right)}^2}}}{2}\)

Dấu bằng xảy ra khi và chỉ khi O’H = O’O hay H ≡ O

⇒ O’O ⊥ MO hoặc O’O ⊥ O’N

Vậy tứ giác MNO’O có diện tích lớn nhất là \(\frac{{{{\left( {R' + R} \right)}^2}}}{2}\) khi O’O ⊥ MO hoặc O’O ⊥ O’N.