Cho tam giác ABC (AB < AC), đường cao AK. Vẽ đường tròn tâm O đường kính BC.
Câu hỏi:
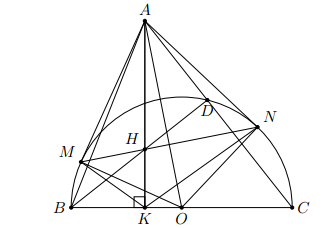
Cho tam giác ABC (AB < AC), đường cao AK. Vẽ đường tròn tâm O đường kính BC. Từ A kẻ các tiếp tuyến AM, AN với đường tròn (O) (M, N là các tiếp điểm; M và B nằm trên nửa mặt phẳng có bờ là đường thẳng AO). Gọi H là giao điểm của hai đường thẳng MN và AK. Chứng minh rằng:
a) Tứ giác AMKO nội tiếp đường tròn.
b) KA là tia phân giác của ^MKN .
c) AN2 = AK.AH.
d) H là trực tâm của tam giác ABC.
Trả lời:
a) AM, AN là tiếp tuyến của đường tròn (O) nên ^AMO=^ANO = 90°
AK là đường cao của tam giác ABC nên ^AKO=^AKC = 90°
Ba điểm M, K, N cùng nhìn đoạn AO dưới một góc vuông nên năm điểm M, K, N, A, O thuộc đường tròn đường kính AO.
Vậy tứ giác AMKO nội tiếp đường tròn.
b) AM, AN là tiếp tuyến của đường tròn (O) nên AM = AN (1)
Theo chứng minh câu trên, năm điểm M, K, N, O, A cùng thuộc một đường tròn nên ta có tứ giác AMKN nội tiếp
Từ (1) và (2) suy ra ^AKM=^AKN (các góc nội tiếp cùng chắn các cung bằng nhau thì bằng nhau). Vậy KA là tia phân giác của ^MKN
c) {^ANH=^AKM^AKM=^AKN ⇒ ^AKN=^ANH
∆ANK và ∆ANH có:
⇒ ∆AHN ~ ∆ANK (g.g)
^AKN=^ANH
^KAN=^HAN
Suy ra: ANAK=AHAN hay AN2 = AH.AK (3)
d) Gọi D là giao điểm của AC và (O)
∆AND và ∆CAN có ^NAD=^NAC,^AND=^ACN (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau) nên ∆AND ~ ∆CAN (g.g)
Suy ra: ANAC=ADAN hay AN2 = AD.AC (4)
Từ (3) và (4) suy ra: AH.AK = AD. AC hay AHAC=ADAK
Xét ∆AHD và ∆ACK có:
{^HAD=^KACAHAC=ADAK ⇒∆AHD ~ ∆ACK (c.g.c)
⇒ ^ADH=^AKC=90°. Dẫn đến (5)
Điểm D thuộc đường tròn đường kính BC nên (6)
Từ (5) và (6) suy ra: B, H, D thẳng hàng
Nghĩa là BH ⊥ AC. Lại có: AH ⊥ BC nên H là trực tâm của tam giác ABC.
