Cho tam giác ABC biết độ dài ba đường trung tuyến lần lượt bằng 15, 18, 27. a) Tính diện tích tam giác ABC.

Cho tam giác ABC biết độ dài ba đường trung tuyến lần lượt bằng 15, 18, 27.

a) Tính diện tích tam giác ABC.

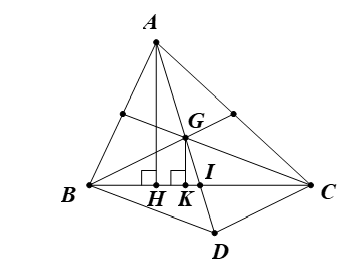
a) Gọi I là trung điểm BC và G là trọng tâm của tam giác ABC.

Suy ra $\frac{AI}{GI}=3$ .

Kẻ AH ⊥ BC và GK ⊥ BC (H, K ∈ BC).

Suy ra AH // GK.

Áp dụng định lí Thales, ta được: $\frac{AH}{GK}=\frac{AI}{GI}=3$ .

Khi đó $\frac{S_{ABC}}{S_{GBC}}=\frac{\frac{1}{2}.AH.BC}{\frac{1}{2}.GK.BC}=\frac{AH}{GK}=3$ .

Suy ra S_ABC = 3S_GBC.

Lấy D là điểm đối xứng với G qua I.

Suy ra I là trung điểm của GD.

Khi đó tứ giác BGCD là hình bình hành.

Suy ra $S_{GBC}=S_{BGD}=\frac{1}{2}{S}_{BGCD}$  .

Do đó S_ABC = 3S_BGD.

Giả sử m_a = 15, m_b = 18, m_c = 27.

Suy ra $\left\{\begin{array}{l}BG=\frac{2}{3}.m_b=\frac{2}{3}.18=12\\ BD=CG=\frac{2}{3}.m_c=\frac{2}{3}.27=18\end{array}\right.$

Ta có I là trung điểm của GD.

Suy ra . $GD=2GI=2.\frac{1}{3}AI=\frac{2}{3}.m_a=\frac{2}{3}.15=10$

Nửa chu vi của tam giác BGD là: $p=\frac{GD+BD+BG}{2}=\frac{10+18+12}{2}=20$ .

Diện tích của tam giác BGD là: $S_{BGD}=\sqrt{p\left(p-BG\right)\left(p-GD\right)\left(p-BD\right)}=40\sqrt{2}$ .

Suy ra $S_{ABC}=3S_{BGD}=3.40\sqrt{2}=120\sqrt{2}$ .

Vậy diện tích tam giác ABC bằng $120\sqrt{2}$ .