Cho tam giác ABC cân tại A, I là giao điểm các đường phân giác trong tam giác. Gọi H là trung điểm của BC, IK là đường kính của đường tròn tâm O. Chứng minh: AI . HK = AK . HI.
Câu hỏi:
Cho tam giác ABC cân tại A, I là giao điểm các đường phân giác trong tam giác. Gọi H là trung điểm của BC, IK là đường kính của đường tròn tâm O. Chứng minh: AI . HK = AK . HI.
Trả lời:
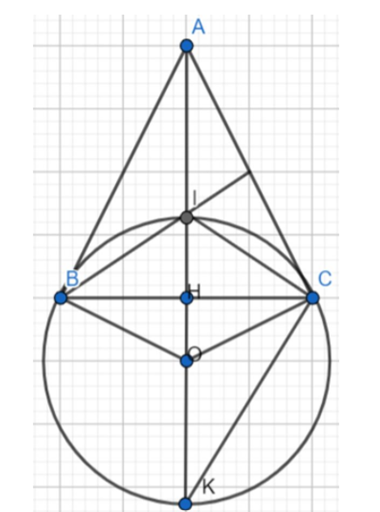
Xét ΔABC có:
CI là phân giác của
CK ^ CI
Þ CK là đường phân giác góc ngoài
(tính chất đường phân giác)
Þ AI. HK = AK. HI (đpcm)
Vậy AI. HK = AK. HI

