Cho tam giác ABC có trọng tâm G. Gọi M là trung điểm BC. Phân tích vec tơ AG theo 2 cạnh
Câu hỏi:
Cho tam giác ABC có trọng tâm G. Gọi M là trung điểm BC. Phân tích theo 2 cạnh của tam giác. Khẳng định nào sau đây đúng?
A.
B.
C.
D.
Trả lời:
Đáp án đúng là: A
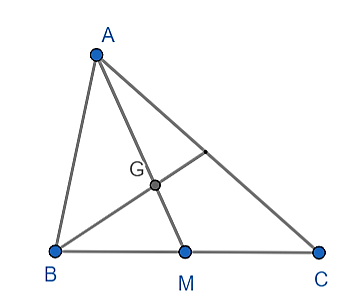
M là trung điểm của BC nên ta có: 2
Vậy .

