Cho tam giác ABC có trung tuyến AM. Đặt vecto a = vecto AB, vecto b = vecto AM
Câu hỏi:
Cho tam giác ABC có trung tuyến AM. Đặt \(\overrightarrow a = \overrightarrow {AB} \), \(\overrightarrow b = \overrightarrow {AM} \). Giả sử \(\overrightarrow {AC} = x\overrightarrow a + y\overrightarrow b ;\,\,x,y \in \mathbb{R}\). Tìm cặp số (x; y) tương ứng.
Trả lời:
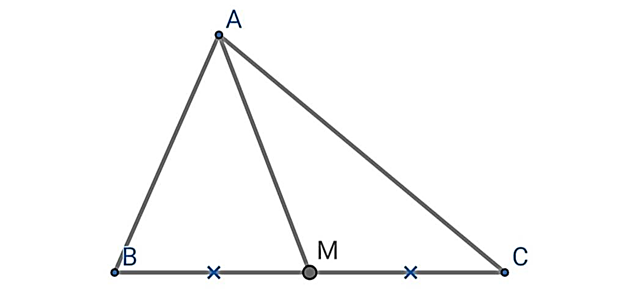
AM là trung tuyến ΔABC
⇒ M là trung điểm BC
\(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \)
\(\overrightarrow {AC} = 2\overrightarrow {AM} - \overrightarrow {AB} \)
\(\overrightarrow {AC} = - \overrightarrow a + 2\overrightarrow b = x\overrightarrow a + y\overrightarrow b \)
Suy ra: (x; y) = (–1; 2)

