Cho tam giác ABC đều cạnh bằng 1, trọng tâm G. Tính độ dài vectơ AG
Câu hỏi:
Cho tam giác ABC đều cạnh bằng 1, trọng tâm G. Tính độ dài vectơ \(\overrightarrow {AG} \).
Trả lời:
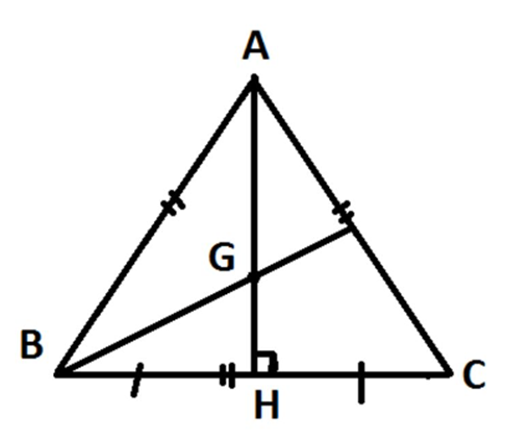
Độ dài của cạnh trong tam giác đều ABC là 1
H là trung điểm cạnh BC
Suy ra: AG = \(\frac{2}{3}AH = \frac{2}{3}\)
Áp dụng định lý Pytago vào tam giác AHC vuông tại H ta có:
\(AH = \sqrt {A{C^2} - H{C^2}} = \sqrt {{1^2} - {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}\)
Suy ra: AG = \[\frac{2}{3}.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{3}\]
\(\left| {\overrightarrow {AG} } \right| = \frac{{\sqrt 3 }}{3}\).

