Cho đường tròn (O), đường kính AB, điểm M nằm trên (O). Vẽ điểm N đối xứng với
Câu hỏi:
Cho đường tròn (O), đường kính AB, điểm M nằm trên (O). Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao điểm của AC và BM.
a) Chứng minh rằng NE ⊥ AB.
b) Gọi F là điểm đối xứng với E qua M. Chứng minh rằng FA là tiếp tuyến của đường tròn (O).
c) Chứng minh rằng FN là tiếp tuyến của đường tròn (B; BA).
Trả lời:
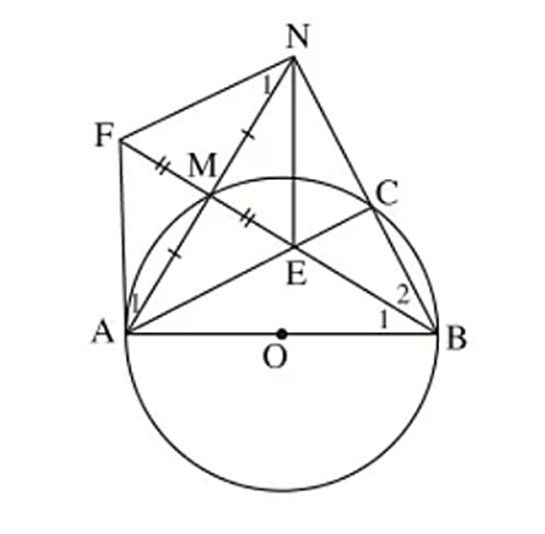
a) Tam giác ABM nội tiếp trong đường tròn (O) có AB là đường kính nên tam giác ABM vuông tại M
⇒ AM ⊥ BM ⇒ AN ⊥ BM tại M
Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên tam giác ABC vuông tại C
⇒ AC ⊥ CB
⇒ AC ⊥ BN tại C
Tam giác ABN có hai đường cao AC và BM cắt nhau tại E nên E là trọng tâm của tam giác ABN
Suy ra: NE ⊥ AB.
b) Ta có:
MA = MN (tính chất đối xứng tâm)
ME = MF (tính chất đối xứng tâm)
Do đó, tứ giác AENF có hai đường chéo AN và FE cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành
⇒ AF // NE
Mà NE AB (chứng minh trên)
⇒ AF ⊥ AB tại A
Vậy FA là tiếp tuyến của đường tròn (O).
c) Trong tam giác ABN ta có:
AN ⊥ BM và MN = AM
Do đó BM vừa là đường cao vừa là đường trung tuyến
Do đó, tam giác ABN cân tại B
⇒ BA = BN
Do đó N thuộc đường tròn (B; BA)
Tứ giác AFNE là hình bình hành
nên AE // FN hay FN // AC
Mặt khác: AC ⊥ BN (chứng minh trên)
⇒ FN ⊥ BN tại N
Vậy FN là tiếp tuyến của đường tròn (B; BA).

