Cho tam giác ABC. Gọi O là một điểm thuộc miền trong tam giác. Gọi M, N, P, Q
Câu hỏi:
Cho tam giác ABC. Gọi O là một điểm thuộc miền trong tam giác. Gọi M, N, P, Q lần lượt là trung điểm của OB, OC, AC, AB.
a) Chứng minh MNPQ là hình bình hành.
b) Xác định vị trí O để MNPQ là hình chữ nhật.
Trả lời:
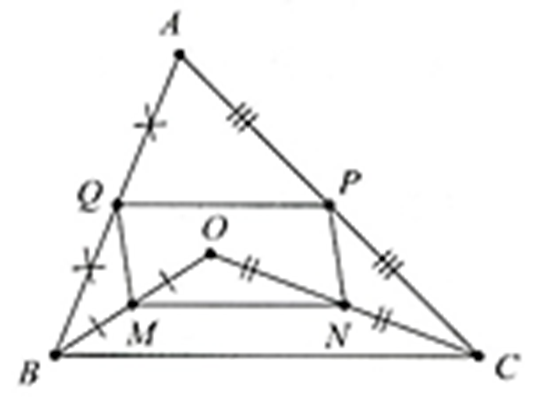
a) Ta có: M, N là trung điểm OB, OC nên MN là đường trung bình của tam giác OBC
Suy ra: MN // BC và MN = \(\frac{1}{2}BC\)(1)
Lại có: Q, P là trung điểm AB, AC nên QP là đường trung bình của tam giác ABC.
Suy ra: QP // BC và QP = \(\frac{1}{2}BC\) (2)
Từ (1) và (2) ta có: MN // QP và MN = QP
Suy ra: MNPQ là hình bình hành.
b) Để MNPQ là hình chữ nhật thì QM vuông góc QP (3)
Mà ta có: QP // BC (4)
QM là đường trung bình của tam giác ABO nên QM // AO (5)
Từ (3), (4) và (5) suy ra: OA vuông góc với BC
Hay O thuộc đường thẳng đi qua A và vuông góc với BC thì MNPQ là hình chữ nhật.

