Cho tam giác ABC, lấy M,N,P sao cho vecto MB = 3 vecto MC , vecto NA
Câu hỏi:
Cho tam giác ABC, lấy M,N,P sao cho \(\overrightarrow {MB} = 3\overrightarrow {MC} ,\overrightarrow {NA} + 3\overrightarrow {NC} = \overrightarrow 0 ,\overrightarrow {PA} + \overrightarrow {PB} = \overrightarrow 0 \)
a) Tính \[\overrightarrow {PM} ,\overrightarrow {PN} \] theo \[\overrightarrow {AB} ,\overrightarrow {AC} \].
b) Chứng minh: M, N, P thẳng hàng.
Trả lời:
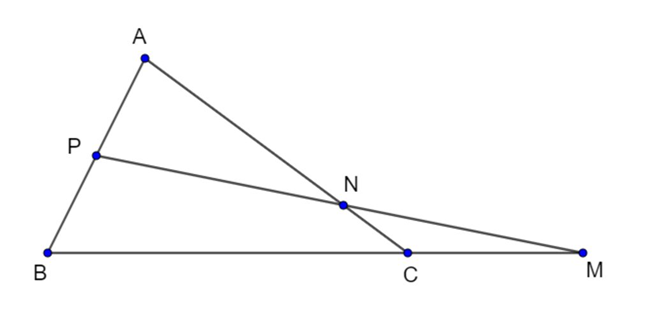
a) \(\overrightarrow {PA} + \overrightarrow {PB} = \overrightarrow 0 \) suy ra: P là trung điểm AB
\(\overrightarrow {AP} = \overrightarrow {PB} = \frac{1}{2}\overrightarrow {AB} \)
\(\overrightarrow {MB} = 3\overrightarrow {MC} \Rightarrow \overrightarrow {CM} = \frac{1}{3}\overrightarrow {BM} \)
Mà \(\overrightarrow {BM} = \overrightarrow {BC} + \overrightarrow {CM} = \overrightarrow {BC} + \frac{1}{3}\overrightarrow {BM} \)
Suy ra: \(\overrightarrow {BM} = \frac{3}{2}\overrightarrow {BC} = \frac{3}{2}\left( {\overrightarrow {BA} + \overrightarrow {AC} } \right) = \frac{3}{2}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)\)
\[\overrightarrow {PM} = \overrightarrow {PB} + \overrightarrow {BM} = \frac{1}{2}\overrightarrow {AB} + \frac{3}{2}\overrightarrow {AC} - \frac{3}{2}\overrightarrow {AB} = \frac{3}{2}\overrightarrow {AC} - \overrightarrow {AB} \]
\(\overrightarrow {NA} + 3\overrightarrow {NC} = \overrightarrow 0 \) nên: \(\overrightarrow {AN} = 3\overrightarrow {NC} \Rightarrow \overrightarrow {NC} = \frac{1}{3}\overrightarrow {AN} \)
Lại có: \(\overrightarrow {AC} = \overrightarrow {AN} + \overrightarrow {NC} = \overrightarrow {AN} + \frac{1}{3}\overrightarrow {AN} = \frac{4}{3}\overrightarrow {AN} \)
Hay: \(\overrightarrow {AN} = \frac{3}{4}\overrightarrow {AC} \)
\(\overrightarrow {AP} = \frac{1}{2}\overrightarrow {AB} \Rightarrow \overrightarrow {PA} = \frac{{ - 1}}{2}\overrightarrow {AB} \)
\(\overrightarrow {PN} = \overrightarrow {PA} + \overrightarrow {AN} = - \frac{1}{2}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \)
b) Ta có: \[\overrightarrow {PM} = \frac{3}{2}\overrightarrow {AC} - \overrightarrow {AB} \]
\[\overrightarrow {PN} = \frac{3}{4}\overrightarrow {AC} - \frac{1}{2}\overrightarrow {AB} = \frac{1}{2}\left( {\frac{3}{2}\overrightarrow {AC} - \overrightarrow {AB} } \right) = \frac{1}{2}\overrightarrow {PM} \]
Suy ra: M, N, P thẳng hàng.

