Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N là điểm chính giữa cung AB, cung
Câu hỏi:
Trả lời:
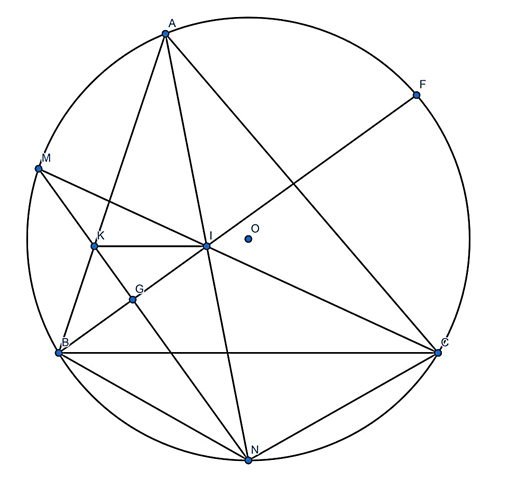
a) Vì M và N lần lượt là điểm chính giữa của cung AB, AC
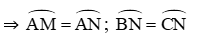
Xét (O)
\(\widehat {ACM} = \widehat {BCM}\) (2 góc nội tiếp cùng chắn 2 cung bằng nhau)
⇒ CI là tia phân giác \(\widehat {ACB}\)
Tương tự trong (O) có \(\widehat {BAN} = \widehat {CAN}\)
⇒ AI là tia phân giác \(\widehat {BAC}\)
Xét ΔABC có:
CI là đường phân giác
AI là đường phân giác
⇒ I là tâm đường tròn nội tiếp ΔABC
⇒ BI là tia phân giác \(\widehat {ABC}\)
Gọi F là giao điểm của BI và (O)
Xét (O) có:
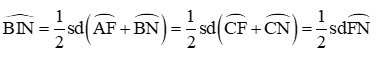
Mà
⇒ \(\widehat {BIN} = \widehat {IBN}\)
⇒ ΔBNI cân tại N.
b) Gọi G là giao điểm của BI và MN
Xét (O) có
\(\widehat {ANM} = \widehat {MNB}\) (2 góc nội tiếp cùng chắn 2 cung bằng nhau)
Xét ΔBIN cân tại N có
NG là đường phân giác
⇒ NK là đường trung trực của IB
⇒ KI = KB
⇒ \(\widehat {KIB} = \widehat {KBI}\)
Mà \(\widehat {ABF} = \widehat {FBC}\)
⇒ \(\widehat {KIB} = \widehat {IBC}\)
Lại có chúng ở vị trí so le trong
⇒ IK // BC.

