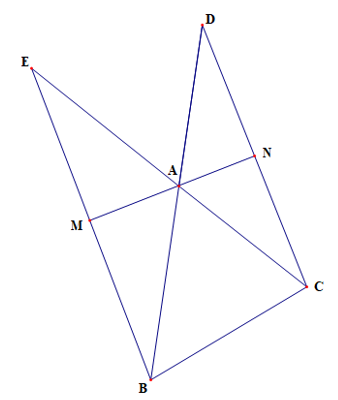
Cho tam giác ABC. Trên tia đối của AB lấy D sao cho AD = AC, trên tia đối của AC lấy E sao cho AE = AB. Gọi M và N lần lượt là trung điểm của BE và CD. Chứng minh 3 điểm M, A, N thẳng hàng.

Cho tam giác ABC. Trên tia đối của AB lấy D sao cho AD = AC, trên tia đối của AC lấy E sao cho AE = AB. Gọi M và N lần lượt là trung điểm của BE và CD. Chứng minh 3 điểm M, A, N thẳng hàng.

Vì AD = AC nên tam giác ACD cân tại A

Mà AN là trung tuyến

Suy ra AN là phân giác của $\widehat{CA\text{D}}$

Do đó $\widehat{CAN}=\widehat{NA\text{D}}=\frac{1}{2}\widehat{CA\text{D}}$

Vì AE = AB nên tam giác ABE cân tại A

Mà AM là trung tuyến

Suy ra AM là phân giác của $\widehat{BA\text{E}}$

Do đó $\widehat{E\text{A}M}=\widehat{MAB}=\frac{1}{2}\widehat{EAB}$

Ta có $\widehat{CA\text{D}}=\widehat{BA\text{E}}$ (hai góc đối đỉnh)

Suy ra $\frac{1}{2}\widehat{CA\text{D}}=\frac{1}{2}\widehat{BA\text{E}}$

Hay $\widehat{CAN}=\widehat{E\text{A}M}$

Ta có $\widehat{CAN}+\widehat{E\text{AN}}=180°$ (hai góc kề bù)

Mà $\widehat{CAN}=\widehat{E\text{A}M}$

Suy ra $\widehat{E\text{A}M}+\widehat{E\text{AN}}=180°$

Hay $\widehat{MAN}=180°$

Do đó M, A, N thẳng hàng

Vậy 3 điểm M, A, N thẳng hàng.