Cho tam giác ABC vuông cân tại A,đường trung tuyến BM. Gọi D là hình chiếu của C
Câu hỏi:
Cho tam giác ABC vuông cân tại A,đường trung tuyến BM. Gọi D là hình chiếu của C trên BM, H là hình của D trên AC. Chứng minh rằng AH = 3HD.
Trả lời:
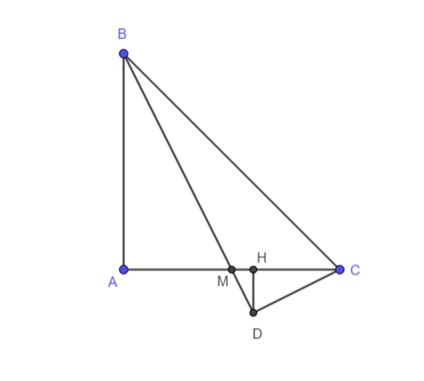
Đặt BA = CA = x
⇒ AM = MC = \(\frac{x}{2};BC = \sqrt 2 x\)
\(BM = \sqrt {B{A^2} + A{M^2}} = \frac{{\sqrt 5 x}}{2}\)
Xét △AMB và △DMC có:
\(\widehat A = \widehat H = 90^\circ \)
\(\widehat {AMB} = \widehat {HMD}\)
⇒ △AMB ∽ △DMC (g.g)
⇒ \(\frac{{MA}}{{MD}} = \frac{{MB}}{{MC}}\)
⇒ MA.MC = MB.MD
⇒ \(MD = \frac{{MA.MC}}{{MB}} = \frac{{x\sqrt 5 }}{{10}}\)
MD2 = MH.MC
⇒ \(MH = \frac{{M{D^2}}}{{DC}} = \frac{x}{{10}}\)
⇒ HC = MC – MH = \(\frac{{2x}}{5}\)
HD2 = HM.HC = \(\frac{x}{{10}}.\frac{{2x}}{5} = \frac{{{x^2}}}{{25}}\)
⇒ HD = \(\frac{x}{5}\)
HA = HM + MA = \(\frac{{3x}}{5}\)
⇒ HA = 3HD
Vậy HA = 3HD.

