Cho tam giác ABC vuông ở A, đường cao AH, biết BH = 9 cm, CH = 16 cm. Tính độ dài các cạnh AB, AC và chiều dài AH.
Câu hỏi:
Cho tam giác ABC vuông ở A, đường cao AH, biết BH = 9 cm, CH = 16 cm. Tính độ dài các cạnh AB, AC và chiều dài AH.
Trả lời:
Lời giải
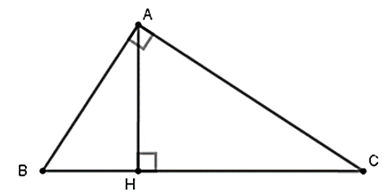
Ta có: BC = BH + HC = 9 + 16 = 25 (cm)
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
AB2 = BH.HC = 9.25 = 225
⇒ AB = 15 (cm)
AC2 = CH.BC = 16.25 = 400
⇒ AC = 20 (cm)
Lại có: AH.BC = AB.AC \( \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{15.20}}{{25}} = 12\) (cm)
Vậy AB = 15 cm, AC = 20 cm, AH = 12 cm
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tìm x, biết: \({x^2} + 5x + 4 - 5\sqrt {{x^2} + 5x + 28} = 0\).
Xem lời giải »
Câu 2:
Cho định lí “Cho số tự nhiên n, nếu n5 chia hết cho 5 thì n chia hết cho 5”.
Định lí này được viết dưới dạng P Þ Q. Hãy phát biểu định lí đảo của định lí trên rồi dùng các thuật ngữ “điều kiện cần và đủ” phát biểu gộp cả 2 định lí thuận và đảo.
Xem lời giải »
Câu 3:
Viết các số (0,25)8 và (0,125)4 dưới dạng các lũy thừa với cơ số 0,5.
Xem lời giải »
Câu 4:
Cho một hộp đựng 4 viên bi đỏ, 5 viên bi xanh và 7 viên bi vàng. Lấy ngẫu nhiên một lần ba viên bi. Tính xác suất để trong ba viên bi lấy được chỉ có hai màu.
Xem lời giải »
Câu 5:
Cho \(\left( {x + \sqrt {{x^2} + 2005} } \right)\left( {y + \sqrt {{y^2} + \sqrt {2005} } } \right) = \sqrt {2005} \). Tính x + y.
Xem lời giải »
Câu 6:
Chứng minh: \(cot{\rm{ }}a--cot{\rm{ }}b{\rm{ }} = \frac{1}{{\tan a}} - \frac{1}{{\tan b}}\).
Xem lời giải »
Câu 7:
Tìm tất cả các giá trị của tham số m để đồ thị hàm số \(y = \frac{{x + 1}}{{\sqrt {{m^2}{x^2} + m - 1} }}\) có bốn đường tiệm cận.
Xem lời giải »


