Cho tam giác ABC vuông ở A(AB
Câu hỏi:
Cho tam giác ABC vuông ở A(AB<AC ) đường cao AH . Gọi D là điểm đối xứng của A qua H . Đường thẳng kẻ qua D song song với AB cắt BC và AC lần lượt là ở M và N . Chứng minh:
a, Tứ giác ABDM là hình thoi
b, AM vuông góc với CD .
Trả lời:
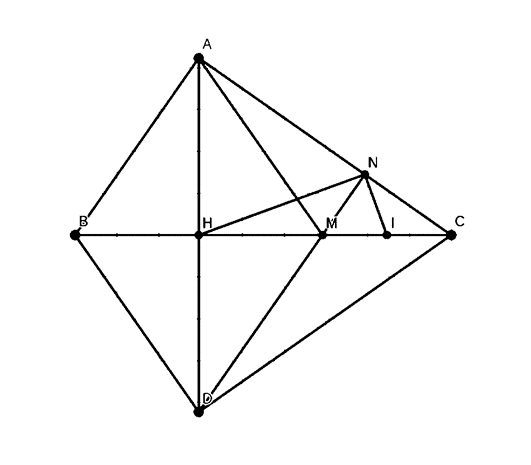
a) Ta có: DM // AB nên \(\frac{{HM}}{{AB}} = \frac{{HD}}{{HA}} = 1\).
Vì HD = HA (giả thiết)
Suy ra: HM = HB
Lại có: AH = HD
Suy ra: AD và BM cắt nhau tại trung điểm mỗi đường nên ABDM là hình bình hành.
Mà AD ⊥ BM nên ABDM là hình thoi.
b) Ta có: DM // AB, AB ⊥ AC
Nên DM ⊥ AC
Mà CH ⊥ AD, CH ∩ DM = {M}
Suy ra: M là trực tâm của tam giác ADC
⇒ AM ⊥ CD
Vì I, H là trung điểm MC, AD
Nên: \[\widehat {INC} = \widehat {ICN} = \widehat {BAH} = \widehat {ADM} = \widehat {HNM}\]
Suy ra: HN ⊥ NI.
Câu hỏi:
Cho tam giác ABC vuông ở A(AB<AC ) đường cao AH . Gọi D là điểm đối xứng của A qua H . Đường thẳng kẻ qua D song song với AB cắt BC và AC lần lượt là ở M và N . Chứng minh:
a, Tứ giác ABDM là hình thoi
b, AM vuông góc với CD .
Trả lời:

a) Ta có: DM // AB nên \(\frac{{HM}}{{AB}} = \frac{{HD}}{{HA}} = 1\).
Vì HD = HA (giả thiết)
Suy ra: HM = HB
Lại có: AH = HD
Suy ra: AD và BM cắt nhau tại trung điểm mỗi đường nên ABDM là hình bình hành.
Mà AD ⊥ BM nên ABDM là hình thoi.
b) Ta có: DM // AB, AB ⊥ AC
Nên DM ⊥ AC
Mà CH ⊥ AD, CH ∩ DM = {M}
Suy ra: M là trực tâm của tam giác ADC
⇒ AM ⊥ CD
Vì I, H là trung điểm MC, AD
Nên: \[\widehat {INC} = \widehat {ICN} = \widehat {BAH} = \widehat {ADM} = \widehat {HNM}\]
Suy ra: HN ⊥ NI.

