Cho tam giác ABC vuông tại A có AB = a, BC = 2a. Tính vecto BC.vecto CA
Câu hỏi:
Cho tam giác ABC vuông tại A có AB = a, BC = 2a. Tính \(\overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {BA} .\overrightarrow {AC} \) theo a?
Trả lời:
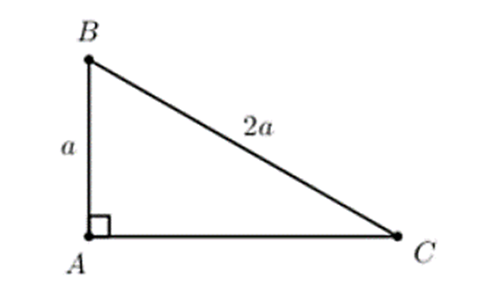
Ta có: sin C = \(\frac{{AB}}{{BC}} = \frac{a}{{2a}} = \frac{1}{2}\)⇒ \(\widehat C = 30^\circ \)⇒ \(\widehat B = 60^\circ \)
Áp dụng định lý Pitago ta có:
AC = \(\sqrt {4{a^2} - {a^2}} = a\sqrt 3 \)
\[\overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {BA} .\overrightarrow {AC} = BC.CA.\cos \left( {\overrightarrow {BC} ;\overrightarrow {CA} } \right) + BA.AC.\cos \left( {\overrightarrow {BA} ;\overrightarrow {AC} } \right)\]
= \(2a.a\sqrt 3 .\cos 30^\circ + a.a\sqrt 3 .\cos 90^\circ \)
= \(2{a^2}\sqrt 3 .\frac{{\sqrt 3 }}{2} = 3{a^2}\).


