Cho tam giác ABC vuông tại A có AB = AC. Gọi K là trung điểm BC. Chứng minh ∆AKB = ∆AKC và AK ⊥ BC
Câu hỏi:
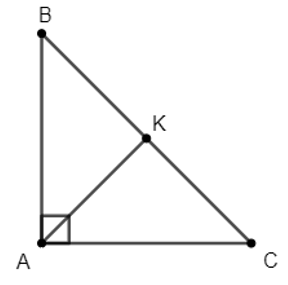
Cho tam giác ABC vuông tại A có AB = AC. Gọi K là trung điểm BC. Chứng minh ∆AKB = ∆AKC và AK ⊥ BC
Trả lời:
Xét ∆AKB và ∆AKC có:
AK cạnh chung
BK = KC (gt)
AB = AC (gt)
⇒ ∆AKB = ∆AKC (c.c.c)
⇒
Vì (hai góc kề bù) (1)
Mà (2)
Từ (1) và (2) suy ra
Vậy AK ⊥ BC (đpcm)
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho tam giác ABC vuông tại A có AB < AC. Gọi D và E lần lượt là trung điểm của các cạnh AC và BC, kẻ EF ⊥ AB tại F.
a) Chứng minh ADEF là hình chữ nhật.
Xem lời giải »
Câu 2:
b) Gọi G là điểm đối xứng với E qua D. Chứng minh tứ giác AECG là hình thoi.
Xem lời giải »
Câu 3:
Cho ∆ABC vuông tại A, có . Gọi M và N lần lượt là trung điểm của BC và AC.
a) Tính .
Xem lời giải »
Câu 4:
b) Gọi E là điểm đối xứng với M qua N. Chứng minh tứ giác AECM là hình thoi.
Xem lời giải »
Câu 5:
Tính diện tích hình thang, biết các đáy có độ dài là 7 cm và 9 cm, một trong các cạnh bên dài 8 cm và tạo với một đáy một góc có số đo bằng 30°.
Xem lời giải »
Câu 7:
Gọi (H) là hình tròn xoay thu được khi cho tam giác đều ABC có cạnh a quay quanh AB, tính thể tích khối tròn xoay giới hạn bởi (H).
Xem lời giải »
Câu 8:
Một hình chữ nhật có độ dài cạnh lần lượt là 15 cm, 12 cm, nếu giảm một cạnh đi 3 cm thì phải tăng cạnh kia bao nhiêu cm để diện tích chữ nhật không đổi.
Xem lời giải »