Cho tam giác ABC vuông tại A có góc BAC = 60°, kẻ tia Ax song song với BC.
Câu hỏi:
Cho tam giác ABC vuông tại A có = 60°, kẻ tia Ax song song với BC. Trên Ax lấy điểm D sao cho AD = DC.
a) Tính các góc BAD và DAC.
b) Chứng minh tứ giác ABCD là hình thang cân.
c) Gọi E là trung điểm của BC. Chứng minh tứ giác ADEB là hình thoi.
d) Cho AC = 8cm, AB = 5cm. Tính diện tích hình thoi ABED.
Trả lời:
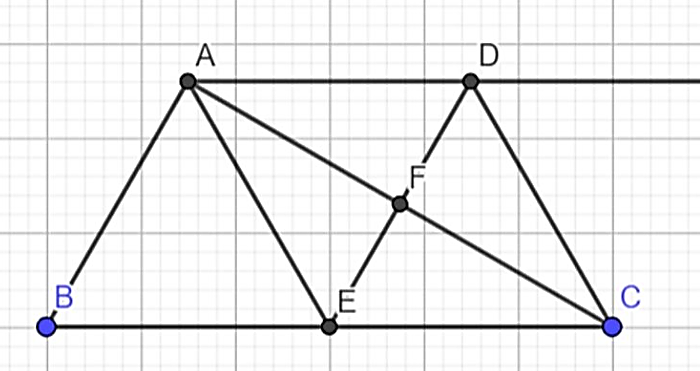
a) Ta có AD//BC
⇒
b) Ta có DA = DC⇒ΔDAC cân tại D
⇒
Mà
⇒
Do AD // BC ⇒ ADCB là hình thang cân
c) Ta có ΔABC vuông tại A, E là trung điểm BC
⇒ EA = EB = EC
Do EA = EC, DA = DC
⇒ DE là trung trực của AC
Gọi DE ∩ AC =F ⇒ F là trung điểm AC
Lại có AD//BC ⇒
⇒ FD = FE ⇒ F là trung điểm EF
⇒ DE ⊥ AC = F là trung điểm mỗi đường
⇒ ADCE là hình thoi
⇒ AD = DC = CE = EA
Ta có AD // BC, AD = BE⇒ ADEB là hình bình hành
Do EA = EB, = 60°
⇒ ΔABE đều
⇒ BA = BE
Mà BA = BE ⇒ ABED là hình thoi
d) Vì ABED là hình thoi
⇒ SABED = 2SABE = SABC = AB⋅AD = 20.

