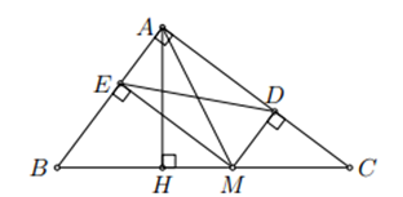
Cho tam giác ABC vuông tại A, điểm M nằm giữa B và C. Gọi D, E thứ tự là hình chiếu của M lên AC, AB. Tìm vị trí của M để DE có độ dài nhỏ nhất.

Câu hỏi:

Trả lời:

Xét tứ giác ADME có $\hat{A} = \hat{D} = \hat{E} = 90 °$

Nên ta có tứ giác ADME là hình chữ nhật, do đó DE = AM.

Khi đó DE_min ⇔ AM_min

Kẻ AH ⊥ BC với H ∈ BC, ta được AM ≥ AH

Suy ra: AM_min ⇔ AM = AH ⇔ M ≡ H ⇔ AM ⊥ BC

Vậy DE_min⇔ AM ⊥ BC

Câu 1:

Cho dãy số: 3; 9; 15; 21; ...; 45; 51. Hãy tính trung bình cộng của các số trong dãy số đó./

Câu 2:

Hiệu của hai số là 308. Nếu lấy số thứ nhất nhân với 5 số thứ hai nhân với 3 thì được hai tích bằng nhau. Tìm hai số đó.

Câu 3:

Hiệu của hai số là 308 . Nếu lấy số thứ nhất nhân với 4 số thứ hai nhân với 3 thì được hai tích bằng nhau. Tìm hai số đó.

Câu 4:

Tính T = (100² + 98² + … + 2²) – (99² + 97² +…+1²).

Câu 5:

Cho tam giác ABC vuông tại A đường cao AH biết BH = 2 cm, CH = 8 cm

a) Tính AH, AB, AC.

Câu 6:

b) Gọi D, E lần lượt là hình chiếu của H lên AB, AC. Chứng minh: HE = 2HD.

Câu 7:

Chứng minh rằng, với mọi n ∈ ℕ*, ta có:

C_{n}^{0} - C_{n}^{1} + C_{n}^{2} - C_{n}^{3} + ... + {(- 1)}^{n} C_{n}^{n} = 0

Câu 8:

Hiệu hai số $\frac{1}{4}$ bằng số bé. Tổng hai số là 279. Tìm hai số đó.

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án