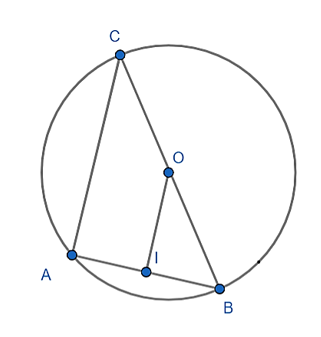
Cho tam giác ABC vuông tại A, nội tiếp đường tròn tâm O, bán kính R = 3cm, biết sinB = 2/3 . a) Hai dây AB và AC, dây nào gần tâm O hơn?
Câu hỏi:
Cho tam giác ABC vuông tại A, nội tiếp đường tròn tâm O, bán kính R = 3cm, biết sin B= .
a) Hai dây AB và AC, dây nào gần tâm O hơn?
Trả lời:
a) Vì ΔABC vuông tại A nội tiếp đường tròn (O; R) nên O là trung điểm của BC.
⇒ BC = 2OB = 2R = 2 . 3 = 6 (cm)
Có ΔABC vuông tại A ⇒ AC = BC. sin = 6. = 4 (cm)
Áp dụng định lí Pythagore vào ΔABC vuông tại A:
BC2 = AB2 + AC2
AB2 = BC2 – AC2 = 62 – 42 = 20
AB = (cm)
Ta thấy: > 4 nên AB > AC suy ra dây AB gần tâm hơn dây AC.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tìm x nguyên để A = có giá trị là số nguyên.
Xem lời giải »
Câu 4:
Tìm x sao cho x4 + 2x3 + 2x2 + x + 3 là số chính phương.
Xem lời giải »
Câu 5:
b) Một đường thẳng qua O, song song với AC cắt AB tại I, tính IB và IO.
Xem lời giải »
Câu 6:
Một tàu hỏa cần chở 620 hành khách. Biết rằng mỗi toa có 12 khoang, mỗi khoang có 8 chỗ ngồi. Số toa ít nhất để chở hết số hành khách trên là bao nhiêu?
Xem lời giải »
Câu 7:
Một người rào xung quanh một mảnh đất hình chữ nhật có chiều dài 28 m, chiều rộng 15m hết 43 cái cọc. Hỏi người đó rào xung quanh khu đất hình vuông có cạnh 25 m hết bao nhiêu cái cọc?
Xem lời giải »
Câu 8:
Người ta xây dựng rào xung quanh một cái hồ hình chữ nhật có chiều dài 45m, chiều rộng kém chiều dài 23,5m, bức tường cao 1,6m. Cứ mỗi mét vuông tiêu tốn hết 40000 đồng. Hỏi xây bức tường rào đó hết tất cả bao nhiêu tiền?
Xem lời giải »