Cho tam giác ABC vuông tại A. Trên AB, AC lần lượt lấy các điểm D, E. Gọi M, N
Câu hỏi:
Cho tam giác ABC vuông tại A. Trên AB, AC lần lượt lấy các điểm D, E. Gọi M, N, P, Q lần lượt là trung điểm của DE, EB, BC, CD. Chứng minh: 4 điểm M, N, P, Q cùng thuộc 1 đường tròn.
Trả lời:
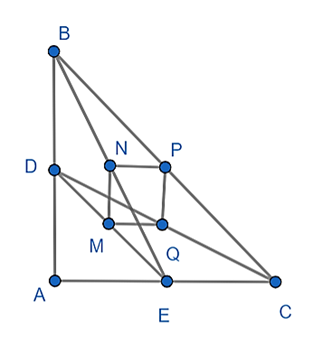
Tam giác DEB và tam giác DCB có MN; PQ là đường trung bình
⇒ MN // PQ và MN = PQ (cùng // BD và bằng \(\frac{{BD}}{2}\))
⇒ Tứ giác MNQP là hình bình hành. (1)
Ngoài ra MQ là đường trung bình của tam giác CDE
⇒ MQ // AC và MN // AB mà AB vuông góc CD
⇒ MN vuông góc MQ
⇒ \(\widehat {MNQ} = 90^\circ \) (2)
Từ (1) và (2) ⇒ MNQP là hình chữ nhật
⇒ M, N, P, Q cùng thuộc 1 đường tròn.

