Cho tam giác AKC cân tại A, đường cao AB, dựng hình chữ nhật ABCM, vẽ BD vuông góc với AC. Gọi F, N lần lượt là trung điểm của CD và AM. Chứng minh KD vuông góc với FN.
Câu hỏi:
Cho tam giác AKC cân tại A, đường cao AB, dựng hình chữ nhật ABCM, vẽ BD vuông góc với AC. Gọi F, N lần lượt là trung điểm của CD và AM. Chứng minh KD vuông góc với FN.
Trả lời:
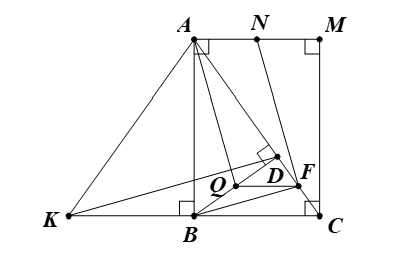
Gọi Q là trung điểm của BD.
Mà F là trung điểm của CD (giả thiết).
Suy ra FQ // BC và (1)
Hình chữ nhật ABCM, có: AM = BC và AM // BC (2)
Lại có N là trung điểm AM. Suy ra (3)
Từ (1), (2), (3), suy ra FQ = AN và FQ // BC // AN.
Do đó tứ giác AQFN là hình bình hành.
Vì vậy AQ // NF (4)
Lại có FQ // BC (chứng minh trên) và BC ⊥ AB (giả thiết).
Suy ra FQ ⊥ AB.
Mà BD ⊥ AC (giả thiết).
Do đó Q là trực tâm của tam giác ABF.
Vì vậy AQ ⊥ FB (5)
Tam giác AKC cân tại A có AB là đường cao.
Suy ra AB cũng là đường trung tuyến của tam giác AKC.
Tam giác CDK có F, B lần lượt là trung điểm CD, KC.
Suy ra FB là đường trung bình của tam giác CDK.
Do đó FB // KD (6)
Từ (4), (5), (6), ta thu được FN ⊥ KD.

