Cho tam giác đều ngoại tiếp đường tròn bán kính 2 cm. Khi đó cạnh của tam giác đều có độ dài

Câu hỏi:

Cho tam giác đều ngoại tiếp đường tròn bán kính 2 cm. Khi đó cạnh của tam giác đều có độ dài bằng bao nhiêu?

Trả lời:

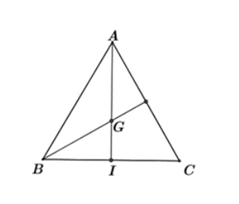
Media VietJack

Tam giác đều ABC nên tâm đường tròn ngoại tiếp trùng với trọng tâm của tam giác

⇒ G là trọng tâm của ABC

Gọi I là trung điểm của BC; AB = AC = BC = a

BI = $\frac{a}{2}$

AI = $\sqrt{A B^{2} - B I^{2}} = \sqrt{a^{2} - \frac{a^{2}}{4}} = \frac{a \sqrt{3}}{2}$

AG = $\frac{2}{3} A I = \frac{2}{3} . \frac{a \sqrt{3}}{2} = \frac{a \sqrt{3}}{3}$

Do: R = AG = 2 nên 2 = $\frac{a \sqrt{3}}{3}$

Suy ra: a = $= \frac{6}{\sqrt{3}} = 2 \sqrt{3}$ (cm).

Vậy tam giác đều có cạnh là $2 \sqrt{3}$ (cm).

Câu 1:

Cho hình thoi ABCD có cạnh bằng a và = 60°. Độ dài của vectơ $\vec{B A} + \vec{B C}$ ?

Câu 2:

Cho tam giác ABC có AB = AC và M là trung điểm của BC. Gọi N là trung điểm của AB, trên tia đối của NC lấy điểm K sao cho NK = NC.

a) Chứng minh ∆ABM = ∆CMA.

b) Chứng minh AK = 2MC.

c) Tính $\hat{M A K}$ .

Câu 3:

Cho tam giác ABC có AB = c, BC = a, AC = b thỏa mãn: b² + c² – a² = $\sqrt{3} b c$ . Tính số đo $\hat{B A C}$ .

Câu 4:

Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 3,6 cm HC = 6,4 cm.

a) Tính AB, AC, AH.

b) Kẻ HE vuông góc AB, HF vuông góc AC. Chứng minh AB.AE = AC.AF.

Câu 5:

Với A, B, C là 3 góc trong 1 tam giác, chứng minh sin A + sin B + sin C = $4 \cos \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}$ .

Câu 6:

Tìm x biết $|2 x + 1| . \frac{2}{3} = 2$ .

Câu 7:

Cho cấp số cộng (u_n) thỏa mãn u₂ – u₃ + u₅ = 10 và u₁ + u₆ = 17. Tìm u₁ và công sai của cấp số cộng sao cho.

Câu 8:

Viết biểu thức bậc ba của 7 +

\sqrt{50}

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án