Cho tích phân 0 1 (1 / (x + 1) - 1/ (x + 2) dx = a ln2 + b ln3 với a, b là các số nguyên
Câu hỏi:
Cho \[\mathop \smallint \limits_0^1 \left( {\frac{1}{{x + 1}} - \frac{1}{{x + 2}}} \right)dx = a\ln 2 + b\ln 3\]với a, b là các số nguyên. Chứng minh a + 2b = 0.
Trả lời:
\[\mathop \smallint \limits_0^1 \left( {\frac{1}{{x + 1}} - \frac{1}{{x + 2}}} \right)dx = \left( {ln|x + 1| - ln|x + 2|} \right)|_0^1\]
\[ = ln\mid \frac{{x + 1}}{{x + 2}}\mid \mid _0^1 = ln\frac{2}{3} - ln\frac{1}{2} = ln2 - ln3 + ln2 = 2ln2 - ln3\]
\[ \Rightarrow \left\{ \begin{array}{l}a = 2\\b = - 1\end{array} \right. \Rightarrow a + 2b = 2 - 2 = 0\]
Vậy a + 2b = 0.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tìm giá trị lớn nhất của hàm số y = x(2 − lnx) trên đoạn [2; 3] .
Xem lời giải »
Câu 2:
Tìm giá trị nhỏ nhất của hàm số trên đoạn \[\left[ {\frac{1}{e};\,\,e} \right]\].
Xem lời giải »
Câu 3:
Tìm số giao điểm của đồ thị hàm số y = x4 − 3x2 − 5 và trục hoành.
Xem lời giải »
Câu 4:
Tìm giao điểm của đồ thị hàm số y = 2x + 1 (d) và trục hoành.
Xem lời giải »
Câu 5:
Gọi S là tập hợp các số tự nhiên có ba chữ số (không nhất thiết khác nhau) được lập từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Chọn ngẫu nhiên một số \[\overline {abc} \] từ S. Tính xác suất để số được chọn thỏa mãn a ≤ b ≤ c.
Xem lời giải »
Câu 6:
Hỏi có bao nhiêu giá trị m nguyên trong [−2017;2017] để phương trình:
log(mx) = 2log(x + 1) có nghiệm duy nhất?
Xem lời giải »
Câu 7:
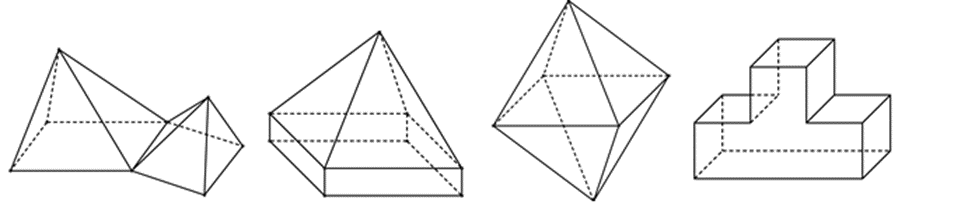
Có bao nhiêu hình đa diện trong các hình dưới đây?
Xem lời giải »
Câu 8:
Cho hàm số f(x) thỏa mãn \[f\left( 2 \right) = - \frac{2}{9}\]và f ′(x) = 2x[f(x)]2 với mọi \[x \in \mathbb{R}\]. Tính giá trị của f(1).
Xem lời giải »